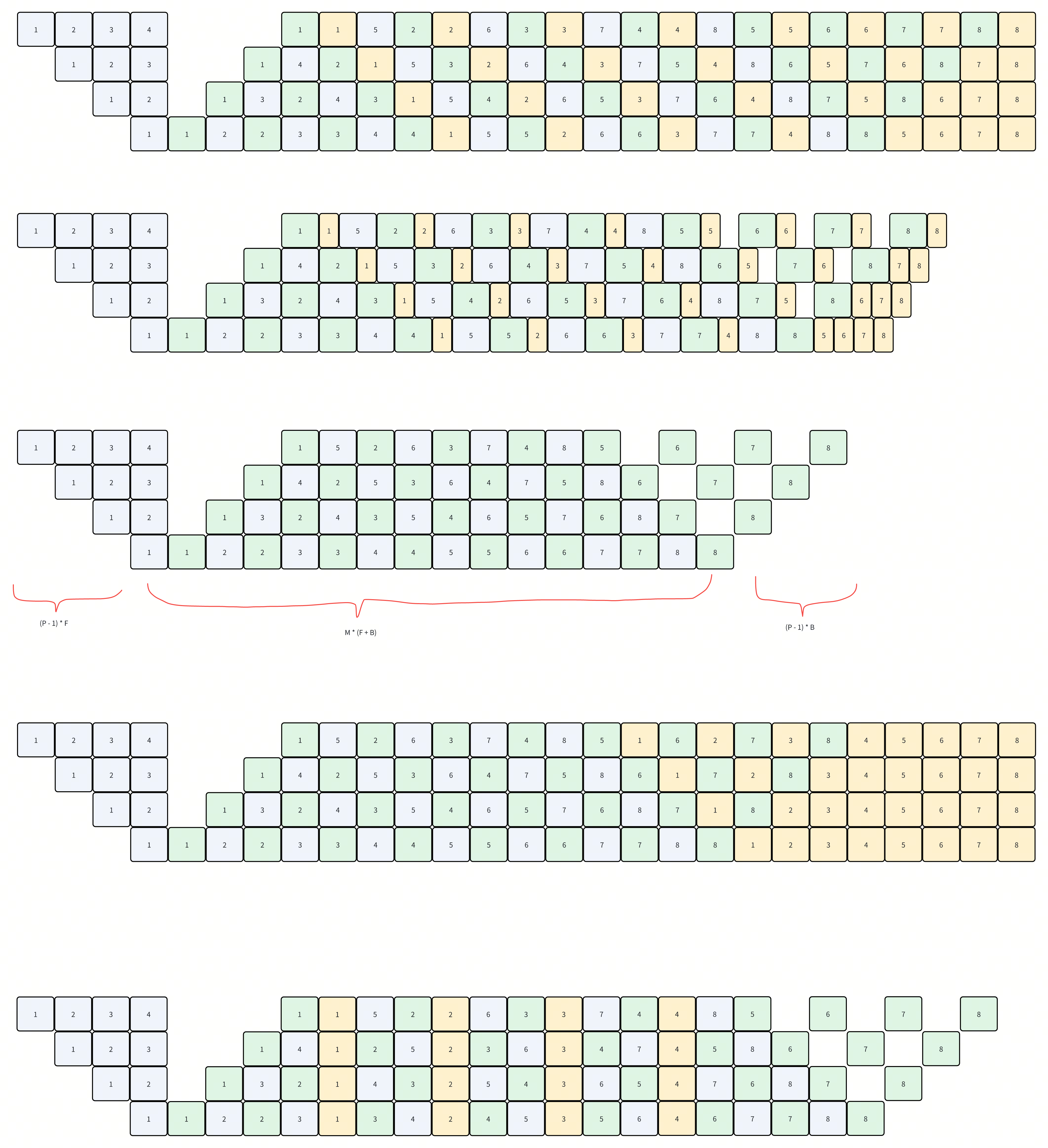
最上面的是zero bubble h1
第二张图是减少T_w之后的调度结果
第三/四张图是不考虑内存的调度结果

bubble的计算逻辑：

• 3是1F1B，不放置w的调度结果。可以看到执行时间是：
  • M * (F + B) + (P-1) * F + (P-1) * B
• 考虑这里的关键我认为在于看最后一个stage，因为最后一个stage没有任何依赖，一直都是跑满的。

• 那么bubble size就是最后一个stage idle的时间，对应的就是图中的(P - 1) * (F + B)

• 这个就得到了1F1B的bubble size，把(B + W)带入B即可

• 拆分W后，因为W没有依赖（严格来说是必须在对应的B之后），所以考虑把W放到图三的后半段，就得到了图四

• 可以这样考虑bubble size的计算：

  • 最后一个rank，每增加一段时间T，bubble size就减少T。因为最后一个rank是满速执行的，相当于增加了有效的执行时间。
    • 按照公式算，bubble size = total - expectation = total - last_rank_execution_time。
  • 对应的，因为total取决于最慢的first rank，所以每增加一段时间T，bubble size就增加T。

• 对于上面图四，最后一个rank从头执行所有的W，所以有效时间增加了 m * W。而first rank额外执行了m - (p - 1)个W。所以total time增加了(m - (p - 1)) * W

  • 之所以减掉了p - 1，是因为cool down阶段，有p - 1个空无法通过新的forward填上，就只能用W来填了。

  • 实际上这里填的时候还应该考虑W的大小，比如如果W远小于F，那可以填很多的W。这里假设是1:1的，所以只能填p - 1个

• 最终计算出来bubble size就少了(p - 1) * W了。对于的就是论文中的式子

然后这里还有一个问题，就是图四并不是对应论文中的ZB-H1，因为我把所有的W都放到了最后，导致峰值内存会比较高。而原文中把W往前推。效果类似于延长了forward的执行时间，然后到cooldown阶段没有新的forward了之后，W的计算就变成了forward，来填补1F1B的空。

• 这里引入了一个问题，为什么是按照forward，为什么不按照其他的方法来放置W呢。

• 为了不影响依赖的话，直观感觉就是三种放置的方式：

  • 跟着forward放，相当于延长forward时间

  • 跟着backward放，变成了原本的1F1B

  • 竖着放，相当于stop the world，所有人都停一会。这种实现起来应该比较复杂，微微一点优势就是提早算一下W。

• 所以这里选择了跟着forward放，并且跟着forward放的话，最后用W填充cooldown阶段的bubble理解也更加直观。

  • 相当于steady state的时候， forward是F + W，cooldown阶段还有forward，forward是W

后面那个2W的还推导不出来。。
直观的理解就是：

• 上面的bubble中，剩下了rank0，在第一个backward之前的bubble。

• 之所以没有用forward填满，是有内存的限制。

• 发起更多的microbatch可以填满这里的bubble，最多需要2(p - 1)个。

• 填满之后，最终的调度的样子会成为ZB-H2的样子，此时如果有optimizer step的同步，还是会有固定的bubble。固定为(P - 1) * F。

  • Optimizer step的同步主要是为了做NAN的检查，以及grad clipping。
• 解决方法就是先做optimizer.step()，然后再去做nan检查，以及grad clipping。因为文章中提到：

However, we noticed that most of the time the global states have no effects, e.g., the global check for NAN and INF rarely trigger because in a robust setting most iterations shouldn’t have numerical issues; the gradient clipping rate is also quite low empirically to justify a synchronization of global gradient norm at every iteration.

• 因为主要用的adamw这种，计算是可逆的，可以从前一个step回退回来

• 当optimizer的同步去掉之后，虽然执行时间上是错开的，但是每个rank都是满速，吞吐上也就是zero bubble了。

zero-bubble-v的这种，直观理解：

• 1F1B这种三角形的调度，内存的瓶颈主要在第一个rank上

• 改成一个v形状，这样第一个backward之后，可以立刻释放rank0的一部分内存。然后再进行第二个microbatch的forward

• V形状的这种，用microbatch把第一个V填满（用2 * (p - 1)个）后，第一个microbatch进入到第二个virtual stage的时候，可以立刻做backward。后面的microbatch的第二个v stage不会被执行。内存也就压低了

• 而非V形状的，需要通过p - 1个microbatch把第一个梯形的区域填满，进入到第二个v stage，然后再需要2 * (p - 1)个microbatch填满这个区域，才会到第一个backward。

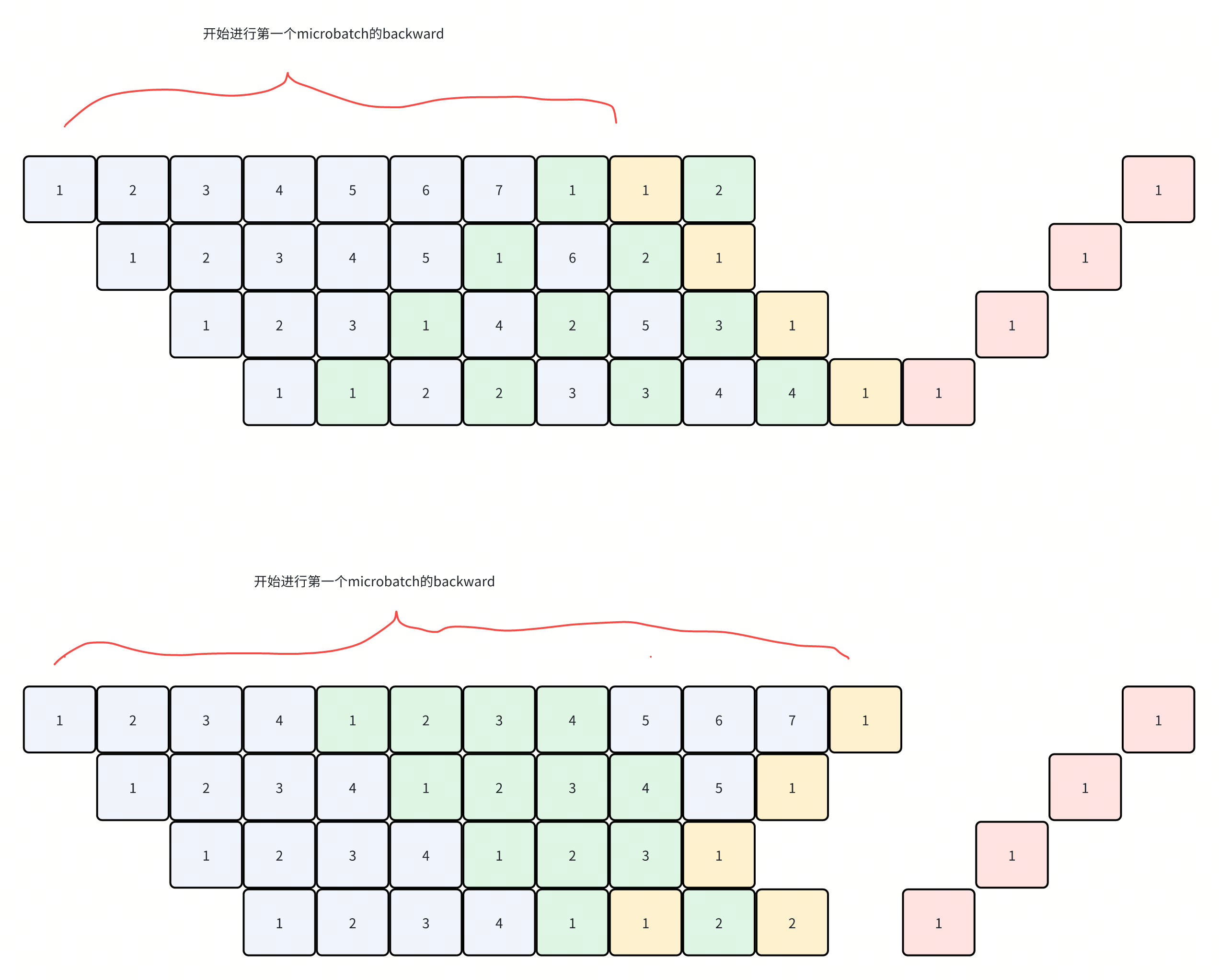
如图，因为图中每一个格子就是一个model chunk + 一个microbatch，所以可以认为内存都是一样的。
从图中的长度就可以看出来峰值内存占用的情况了

Exp

不过torch这里的实验结果看起来差不多
https://discuss.pytorch.org/t/distributed-w-torchtitan-training-with-zero-bubble-pipeline-parallelism/214420

而且内存也高一些，不知道是什么情况。