minhash & LSH

主要来自cs336的lecture和assignment

要做近似去重，用了类似bag of gram的思想。定义两个文档的jaccard similarity是文档中词的交集的数量除以词的并集的数量。

jaccard simiarity大于阈值的时候，就认为文档比较相似，会被过滤掉。

但是jaccard similarity是两两计算的，复杂度是平方级别的，无法很好的拓展。

定义文档的minhash为所有gram的hash值的最小值。

这里有一个比较有意思的结论是:

证明思路也比较简单：

假设两个document，一个是1, 2, 3, 4，另一个是1, 2, 3, 5。
先把所有的grad都通过hash计算一个值出来。每一个grad都有相同的概率变成min。

对于这5个值，如果1, 2, 3是min，那么minhash(A) minhash(B)，因为min相同
如果4, 5是min的话，那么minhash(A) != minhash(B)

minhash冲突的概率就是jaccard similarity。

这里有意思的点在于希望控制冲突的概率，和平常使用hash避免冲突是相反的。和LSH的思想是一样的

这样hash到同一个桶的文档就可以做两两的比对了，减少两两比对的次数。

但是这里冲突的概率是jaccard similarity，比如我们设置threshold为0.7，那么还是会有一些文档有概率没有出现冲突，导致漏掉一些重复的文档。

此时我们就希望让jaccard similarity大于阈值的文档尽量hash到一起，jaccard simiarity小于阈值的文档分散开

这里也借鉴了一下LSH的思想，用多个hash的函数。对于每一个文档，构建出N个minHash的值，然后按照K个一组进行分组放到不同的bucket中。再去对同一个bucket的文档做细粒度的校验

直观理解这个的思路是：
* 当组的数量提高的时候，即便比较小的jaccard similarity也可能会判断到一起，因为组之间是一个OR的语义。只要任意一个组产生了冲突，就可以做细粒度的校验
* 而组内minHash数量提高的时候，就要求比较高的jaccard similarity。因为需要多个minhash都相同。

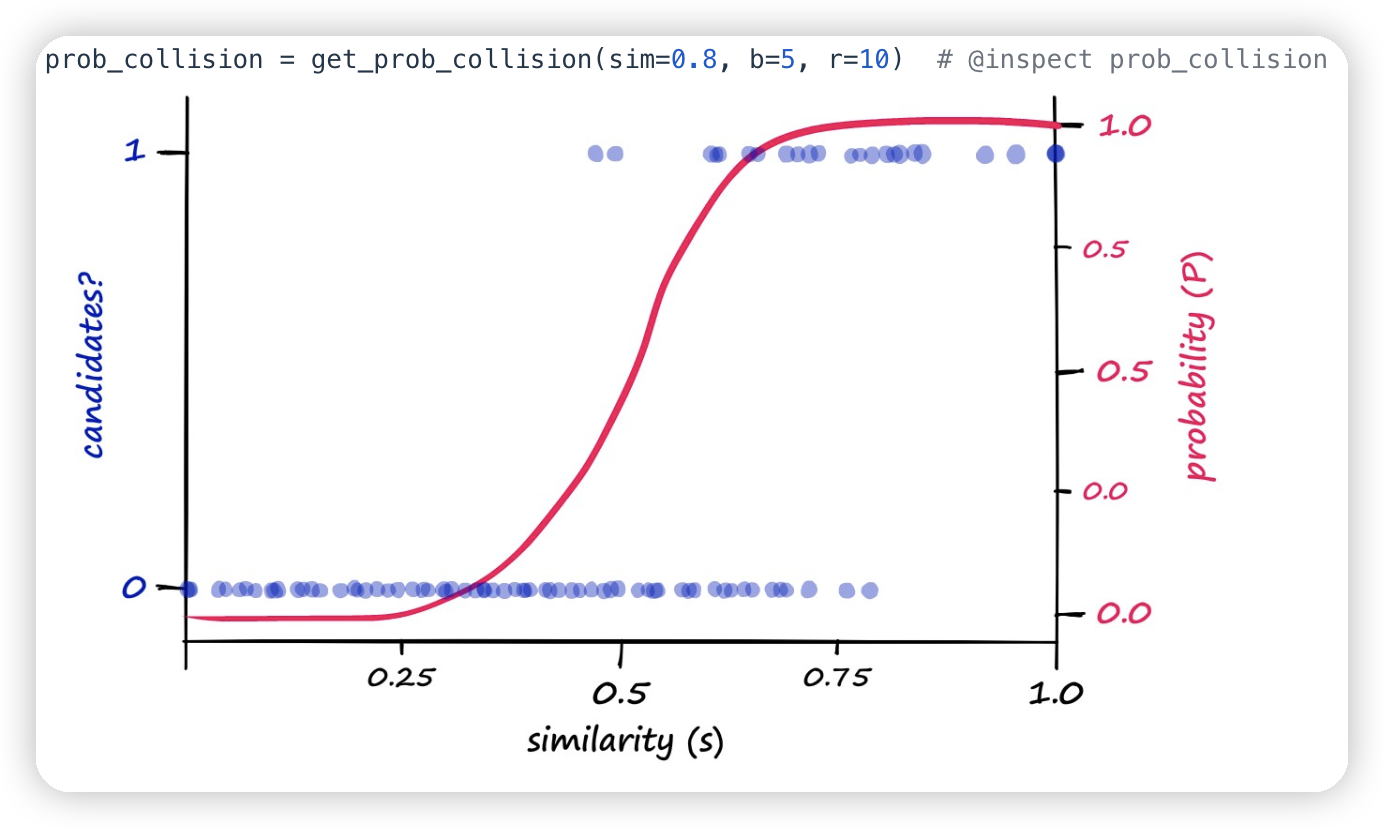
可以得到一个类似这样的曲线。从而让高相似度的文档的冲突概率很高，低相似度的文档不容易冲突。

这个就需要去调整K/N的值。可以解析上面的式子做计算，或者是做一些实验选择合适的参数。