Integrating Compress and Execution in Column-Oriented Database Systems
Abstract
列存储的数据库可以提高相邻数据项之间的相似度,从而带来更好的压缩效果。
压缩的最好方式不仅取决于数据的属性,还取决于查询的workload(sql workload)
Introduction
列存压缩的一个优势就是我们可以在压缩的数据上直接应用算子,从而提高CPU的性能。对于RLE(游程编码)来说,比如他把数据压缩成(42,1000),表示有1000个值为42的数据项。那么我们可以快速计算出他的SUM,而从避免了后续的扫描。
主要点:
* 总揽数据库的压缩算法,并说明他们是怎么被应用到列存的系统中的。并且对比专门用于列存的压缩算法
* 通过实验说明这些算法的tradeoff,并且构建了一个决策树来帮助决策要怎么进行压缩
* 介绍一个可以将算子直接应用在压缩数据上的执行器的架构
* 说明列存中order的重要性
Related Work
前人的工作指出了将压缩算法的具体实现和数据库实现代码隔离开的关键性。通常来说我们可以通过在数据到达算子之前将他们解压缩来实现。但是某些情况下我们可以通过将算子直接应用在压缩的数据上来提高性能。本文的工作就是提出了在提供隔离性的同时,还能从这些优化中获得性能提升的一种方案。
(即算子和压缩模式的解耦)
(其实我比较好奇的是行存的数据库是怎么压缩的呢?RLE的可能性比较小,感觉要么是根据attribute来做dictionary compression,要么是写盘前来把数据看成未解释的字节,然后应用一些压缩算法,基于滑动窗口什么的)
C-Store Architecture
C-store中一个table会被表示为若干个projections。每个projection都由若干个列组成,存储为有序的列存格式。每一列至少在一个projection中,并且一列数据可以在多个projection中存储(这么看起来他应该不会关注跨越projection之间的关系?或者是存储对应的ID来重组整个元组)
他这里说了不同的projection之间是通过join indices来关联的。join indices就是一个排列,可以把一个projection的元组映射到另一个上。(这就带来了两个问题,排列所带来的映射应该是单向的,而我们可能需要双向的映射,还有就是他只能用于两个对象,所以对于多个projection的时候,带来的复杂度是n^2的,但是好处就是我们可以很快速的找到一个projection对应另一个projection的元组,而不需要根据index来进行整个的扫描,即space/computation的tradeoff。不过这样想貌似插入的开销也很大,因为需要重构permutation)
C-store实现了大多数的列版本的关系算子。他和传统的关系算子不同的有:
* selection算子生成的是bitmap,然后一个特殊的mask算子可以根据bitmap和列来进行物化数据得到结果
* 特殊的permute算子,通过之前说到的join index来重排序一个列(从而让他们对应)
* 投影是免费的,因为直接输出列就可以,不需要改变数据(对比row-store,我们得到元组后需要根据output schema重构这个元组)
* join得到的是position,而非value,后面会说为什么(我猜得到的可能是index pair,这样我们可以在推迟物化,从而根据后面的投影来进行物化?)
Compression Schemes
Null Suppression
核心思路就是数据中连续的0或者空白会被替换为一个描述信息,用来描述这些null值的有多少,他们存在哪里。(类比存图的CSC/CSR format,就是只存储有用的信息)
本文中他们实现的思路更加的细粒度,比如一个整数是4个字节。但是可能不需要4个字节就能存储这个整数。所以他们存储了额外的信息,用2位来表示后面的整数是用多少字节存的。从而节省空间(这里应该就是把我们没用到的那些前缀的0给压缩起来,我还以为是以属性为粒度,但是这里用的是数据粒度的)
Dictionary Encoding
将常出现的数据替换成更小的编码,一个例子就是三个颜色"green", "yellow", "red",可以被替换成0, 1, 2。从而节省空间
row-store中的这种压缩方法有一个缺点,就是只能映射单个元组的一个属性。比如一个tuple中的"green"替换成了一个byte 0。然而实际上我们只需要2位就可以完整的表示颜色这个属性。但是不同的元组之间不能混合起来存,所以导致我们就必须通过一个byte来存颜色这个属性。
而column-store的一个好处就是他可以把不同的tuple的属性混合起来压缩,比如刚才的例子,我们就可以让一个byte来存4行的颜色属性
决策要怎么进行压缩的时候的一个考虑点就是我们希望字典能够fit in cache。比如我们的值域是32,用5位来压缩。如果我们用2byte来表示3个value的话,查找的时候就可以直接用这2byte去索引字典。对应的就是32 x 32 x 32种情况,也就是这么大的数组
这种压缩还有一个好处,就是我们可以很容易获得单个tuple的压缩后的数据,从而可以让我们实现在压缩数据上的计算

而且还可以延迟解压缩的过程,从而节省空间
还有一个tradeoff就是没有选择order preserving的压缩方法,因为这通常导致了变长的字典项,从而失去了拥有定长字典项的优势(快速检索单个项,以及byte alignment)
Run-length Encoding
在row-stored的系统中,RLE只能压缩那些大的有很多空格的,或者重复的字符串,即针对单个属性
而排序的列存中则更容易进行压缩。因为我们更容易找到相同的值
Bit-Vector Encoding
当列的值域比较小的时候,我们可以通过这种方式编码。(其实就是位图编码,对每个属性记录他在那行出现)

然后我们可以继续压缩这个位图编码,然而最近研究表示bitmap只有相当稀疏的时候性能才不会受到这个额外的压缩的影响。
然而我们只有在列的基数(意思应该是不同值的个数)小的时候才用这种方法,所以vector相对比较密集
Heavyweight Compression Schemes
Lempel-Ziv Encoding,一个常见的无损压缩算法。他使用滑动窗口动态的构建pattern table,基本思路就是他将输入的序列划分成不相交的变长的block,并且构建block的字典。当后续遇到这些block的时候就会把它替换成指向前面block的一个指针
Compressed Query Execution
Query Executor Architecture
为每个新增的压缩算法添加两个类。一个类包装了压缩的数据,叫做compression block。一个compression block包含了一个有压缩数据的buffer

并通过table1中的API来访问数据
我们可以通过getNext来获得数据,他会解压缩下一个数据,并返回那个值,以及对应的值在正常的列存中的位置。另一个方法就是asArray,会解压缩整个缓冲区,并返回一个指向未压缩数据的指针
block information是我们可以在不去解压缩数据之前就可以获得的信息。比如对于RLE来说,我们可以直接获得数据的大小,以及他们的起始和结束的位置。
对于bit vector来说,一个block里存的就是一个value以及对应的bit vector。所以我们称bit vector block为 non position-contiguous block,指的就是得到的值的位置不是连续的
对于另一个类来说,则称为DataSource operator。DataSource operator是作为query plan和storage manager的接口来使用的,并且含有一些特定的信息,比如压缩的页是怎么存储的,那些索引是有效的等。所以他可以作为一个scan operator,用来从磁盘中读取压缩的数据,并转换为Compressed block
selection的谓词可以被下推到DataSources中,比如字典压缩,DataSource就可以把谓词的值也压缩起来,然后直接在压缩的数据上来应用(这么看起来DataSource也有遍历元组的能力,只不过主要还是读取数据,然后返回compressed block,compressed block就作为iterator来使用,所以一个是算子,一个是算子返回的值。相当于是一个tradeoff了,因为我们可以把压缩这个抽象放到table iterator中来做,这样不需要更改现有的执行引擎。但是我们希望算子可以应用到压缩数据中,所以就把它拉了出来做成了一个额外的算子,这样就可以得到谓词的信息,从而实现在压缩数据上的计算。不过这里有个问题,如果DataSource返回的是compressed block,然后我们需要再得到tuple,为什么不直接让他返回tuple呢?但是如果把compressed block做成抽象的iterator,那暴露给上层的东西是不是太多呢?也可能有特定实现的算子专门使用compressed block,从而把compression和正常的执行隔离开)
Compression-Aware Optimization
他这里说了应该是把算子都修改了,所以有n个压缩算法就会有n个对应版本的算子。
虽然不会影响性能,但是会导致代码复杂度变高。并且有多个输入的算子的复杂度会变得更大。
通过优化join来演示这种问题,我们在做join的时候,可以只挑选需要做join的两个列,然后得到若干个position pair(和我上面预测的一样)
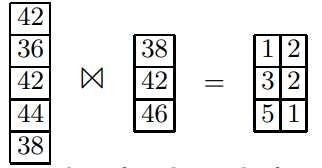

这个算子的伪代码
可以看到当压缩的方法变多的时候,我们的代码复杂度也会越来越高
所以通过compression block来抽象上面的过程。
当算子不能直接在压缩的数据上应用的时候,他就可以通过之前提到的getNext等方法来获得原始数据,正常操作。而当他可以在压缩的数据上操作的时候,他就可以利用block information来优化操作

比如这个count的例子。这里是count t,并且根据c1分组
可以看到他就可以通过IsOneValue来做优化。这样虽然RLE和bit vector是不同的压缩方案,但是在代码中不需要进行区分。
(这个抽象做的很棒,识别了compression data的优化需要的必要信息,并给出了对应的接口。间接看出来做这种抽象要求我们对被抽象者,以及使用抽象接口的地方都要有很深的理解)
(所以这里也能看出来,compressed block的作用是抽象压缩数据的使用,而DataSource operator则是抽象数据的读取,从而生成compressed block)
这个地方的原文很不错我贴一下:By using compressed blocks as an intermediate representation of data, operators can operate directly on compressed data whenever possible, and can degenerate to a lazy decompression scheme when this is impossible. Further, by abstracting general properties about compression techniques and having operators check these properties rather than hardcoding shielded from needing knowledge about the way data is encoded. They simply have to condition for these basic properties of the blocks of data they receive as input.
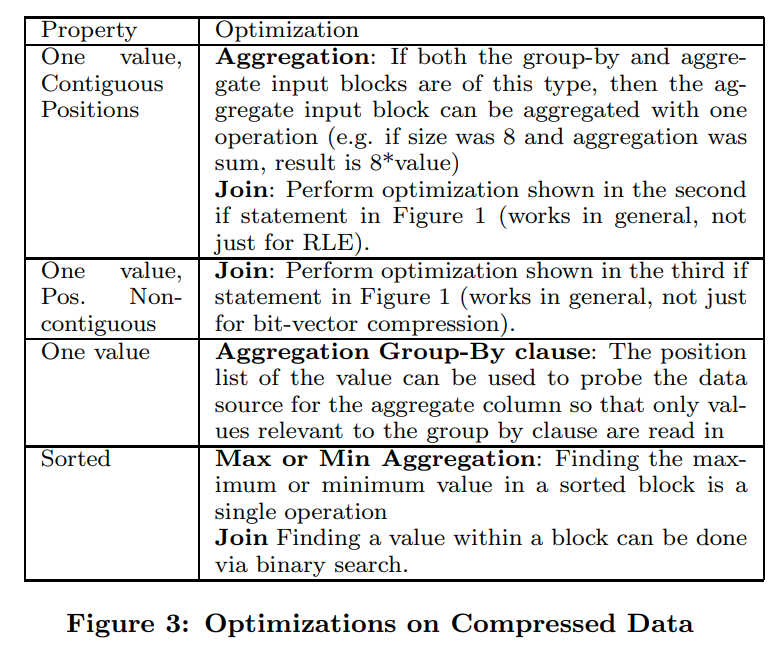
这个图是更一般化的优化技术,第一个的优化我感觉需要group by和aggregate value需要是同一个顺序的。
文章评论