Optimal Column Layout for Hybrid Workloads
Abstract
现代的analytical system是基于列存储。然后通过delta store来进行插入和更新
我们通过确定分区的数量,他们的大小和范围,以及缓冲区大小以及他们是如何分配的来组织数据的分布。
给出workload knowledge以及performance requirements,给出一个优化的物理布局
Introduction
目前的系统对于数据的布局都是固定的,这意味着他们会被局限在某个地方,而不能根据workload来达到比较好的效果。
而我们的insight则是这些设计决策不能被限制在一个先前的决定中,即在设计系统的时候就固定了这些决策。我们可以学习这些决策并且调整他们从而支持HTAP的workload
在这个paper中,我们关注三个比较关键的决策:
1. 数据的物理布局
2. 列存储是否是密集的
3. 怎么为更新操作分配buffer(delta store还是ghost values)
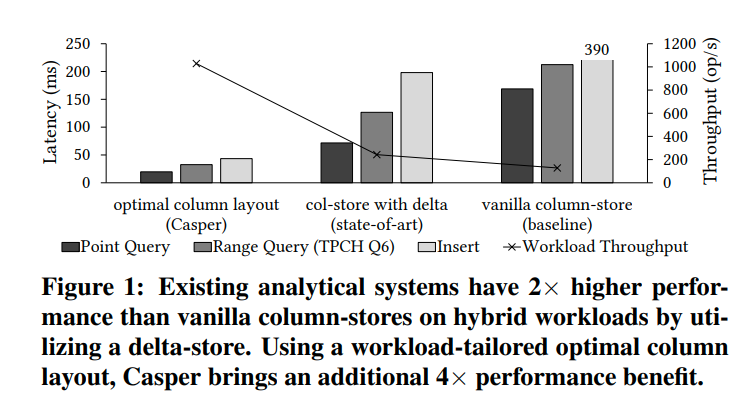
Channenge:
1. Fast Layout Discovery。可以看到我们有很大的提升,但是这不是没有代价的。找到这个优化的布局是一个比较昂贵的操作。最坏情况下有指数级别的数据布局需要我们去枚举以及评估。我们将这个问题转化成binary optimization problem,并且用现成的solver来求解。并且利用数据是存储在column chunk的特性,我们为每个chunk单独的进行优化,从而降低复杂度
2. Workload Tailoring。我们需要有一个比较有代表性的workload的sample。然后分析数据的访问频率以及访问模式。
3. Robustness。当去优化layout的时候我们可能有过拟合的风险
我们针对的是analytical application,有着比较稳定的workload。我们的工具会分析workload,并离线的准备好data layout。类似现代系统的index advisor
他说支持service-level agreements,这个的意思应该是说保证给用户提供什么样的performance(应该和前面对应的performance requirement相关)
Column Layout Design Space
Casper(就是本文的系统)有很大的设计空间:
1. 使用range partitioning作为额外的模式(现有的是根据key排序,或者根据插入顺序排列)
2. 支持原地的,非原地的,以及混合的更新
3. 支持无缓冲,全局缓冲,以及per-partition的缓冲

这里提到存储的scheme和buffer是正交的。还提到了水平分区和垂直分区,我感觉应该就是切分行以及切分列。并且他还支持tiles(不清楚是什么)和projection。对于projection来说,意思应该是读负载可以被projection分摊开,并且不同的projection还可以用不同的layout来得到更好的性能
分区数量也是一个比较关键的因素。
可以看这个图
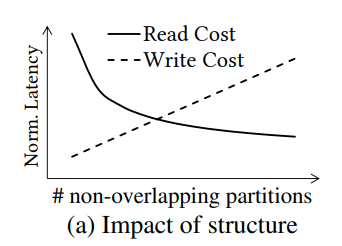
比如说对于一个column chunk,里面有Mc个元素。我们有k个不相交的分区。那么读的开销大概就是Mc/k,而插入(删除)的开销则平均是k/2(因为我们可能需要跨分区移动一些数据)
所以对于读负载,他喜欢更大的分区数量(因为只要读一个分区),而写负载则更喜欢小的分区数量(因为不需要跨越很多分区去修改)
并且对于只读的负载,如果不同的区域有着不同的访问模式,那么等宽的分区可能就会导致不必要的读。对于不常访问的地方,粗粒度的分区就足够了
所以理想情况下,局部优化的分区策略可以让一些有skewed access的workload达到理想的性能(对比则是均衡access的workload)
Ghost Values。当更新数据的时候,如果我们放松对于整个column都有序的这个要求,那么就可以减少数据的移动。对于一个删除操作来说,他只需要找到对应的partition,然后把对应的数据标记为删除即可,从而引入了empty-slot。为了更好的利用,我们可以把empty slot移动到partition的最后面,从而直接处理到来的插入请求。
这些empty slot就叫做ghost value,需要额外的维护,但是可以使更新操作更容易。Ghost value减少了更新的代价,但是带来的是额外的内存使用。trading space amplification for update performance
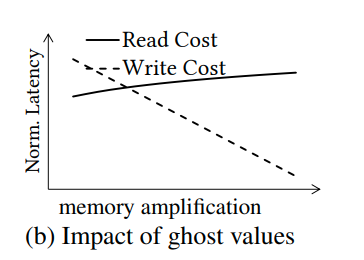
这个是通过增加buffer space来减少写的开销,代价是读变慢(如果每次都是把empty slot放到最后,为什么读会变慢呢?因为缓存吗?)
我们通过考虑数据区域的访问模式分布来达成细粒度的决策(it takes into account the access pattern distribution with respect to the data domain)。casper收集每一种操作访问分布的直方图,并传给我们的cost model
Accessing Partitioned Columns
下面,假设我们有k个可变大小的分区,以及一个轻量级的k叉树作为索引
Point Queries。点查询就是在索引上先确定我们要找的分区,然后分区内部顺序扫描一下。一旦找到我们就可以返回这个值,或者元素的位置(那要是后面变了怎么办?),作为后面算子的输入
Range Queries。首先通过索引找到区间的起始的分区以及结束的分区,然后通过范围过滤一下。中间的分区则可以直接复制给后面的算子
一个演示

Inserts。通过ripple-insert algorithm,来达成O(k)的插入一个元素到分区的操作。
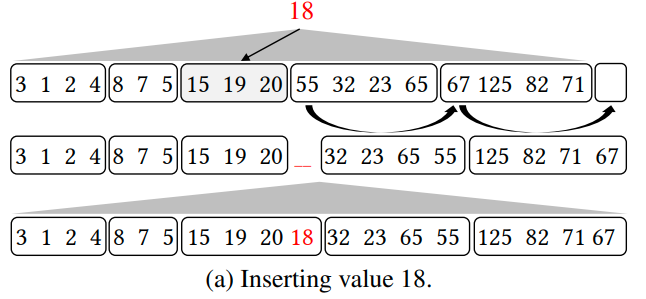
ripple-insert把一个empty slot从column的最后移动到对应的partition中。我们插入到这个empty slot中,并且修正index中刚才移动的partition的边界。
Deletes。对于删除来说,首先就是通过index来确定对应的partition,然后删除对应的元素,并得到一个empty slot。我们根据上面的步骤,再一步一步把empty slot移动到column的末尾。当然也要修正index
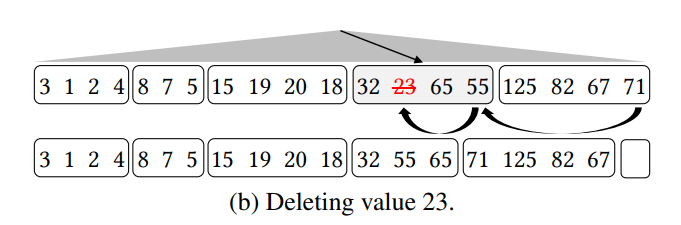
update通过delete加insert来完成
Modeling Column Layouts
总共是5个操作,不同的决策对于不同的操作影响都是不一样的。我们首先考虑没有ghost value的情况
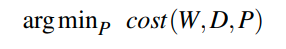
要优化的问题考虑了dataset以及workload。我们需要考虑数据的分布,然后在此之上覆盖访问模式,从而得到effective access distribution
Representing a Partitioning Scheme
通过用位向量来标记分区的边界,从而表示一个分区的模式
一个列由Nb个大小相同的块组成。块的大小是和column chunk的大小一起决定的。我们通过Nb个布尔变量表示分区模式。当一个块的终点作为一个分区的终点的时候,我们把对应的变量设为1

一个示例,所以分区的大小要和block大小对齐?
block的大小是cache line大小的整数倍,最小就是一个cache line,从而可以影响我们分区的粒度。
The Frequency Model
基于上面的Partition Scheme上来介绍访问模式的表示
访问的数据会以logical block的形式整理起来,每一个block中的每一个操作的访问模式都被记录下来。logical block的大小是可变的
我们记录那些block都被那些operation使用了,从而构成若干个直方图,我们称这个直方图为Frequency Model。因为他存储的是每一个区域数据访问的频率
FM利用了10个直方图:

每一个block都有这样的10个counter。最后的直方图的每一块都对应了一个block。
在sample workload上生成直方图的时候,我们不会真正的去计算结果,而只是去捕捉访问模式(更新counter)

这里的更新,当从3到16的时候,empty slot是向前,所以更新的是udf和utf。否则就是udb和utb
虽然示例是一个列,但是我们可以把它放入多个列(但是只能根据一个排序)。因为FM不会在意他内部具体存储的数据(也就是不在乎一个数据项内存的都是什么,只关注block的访问模式)

我们也可以从现有的access pattern中学习FM。我个人感觉就是有了访问每个block的分布了,然后把它转换成直方图而已
Cost Functions
假设数据集中有M个值,block size为B,则我们最多可以有M/B=N个partition
假设访问block有四种IO方式,随机读RR,随机写RW,顺序读SR,顺序写SW
Range Query
他这里给了个例子我觉得还挺有意思的

这个图中,每次我们的RQ尝试从第三个block开始读的时候,如果P1没有设置(在这里没有分区),那么我们就需要额外读第二个block,如果P0也没有设置,那我们就需要额外读第一个block。而如果P1设置的话,我们就不需要进行额外的读,最多读一个block就可以
那么一个block作为开始块进行访问的代价就是
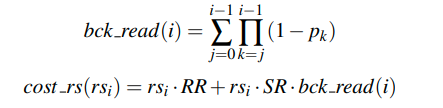
其中第一项表示的是第一次随机读到这个块。而第二项则表示的是由于没有分区导致的额外的block reading,不过这些是顺序读
第二项是累乘的,比如对于第5个block,他前面的就是(1-p4) + (1-p4) * (1-p3) + (1-p4) * (1-p3) * (1-p2)这样的。因为只要后面的分区了,前面就不会有影响
(从这里看大概可以明白他的思路,以block为粒度来分区,然后根据每个block分区或者不分区来计算操作的代价。变量只有每个block是否分区,就变成了01规划,最后我们可以得到一个好的分区方案)
对于block作为结束块的代价是类似的
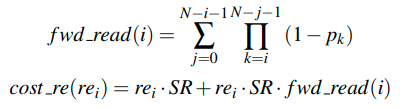
也就是说我们只需要往后找就可以,但是这里最后一块也是顺序读
对于中间块的访问,则是顺序读

所以总和起来,所有的RQ的代价就是
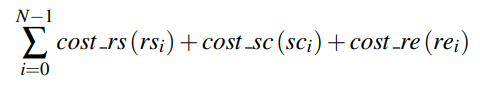
Point Query
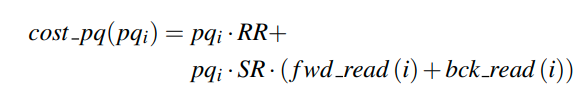
有了前面的例子这里就会容易很多。fwd_read就是向前,也就是下标增大的方向额外读取的block,bck_read则是向下标减少的方向额外读取的block
所以这里代表的是找到partition是一个RR,然后读完是若干个SR
Inserts

因为我们需要从最后面引入一个empty slot,所以我们的后面每有一个partition都会导致一次额外的交换,即读第一个元素,写入到最后一个元素的后一个位置,这里的加一指的是最后一个分区的读写(他的最后一块应该没有标志分区)
Deletes
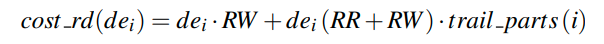
delete和insert十分类似。不同的点就是我们需要一次点查询来得到要删除的数据
这里和insert不同的地方就是我们少一次RR,因为删除的时候直接覆盖就行,不需要知道之前的值的内容。(其实代价算在了点查询中)
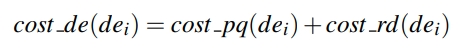
Updates
很多的系统中,update是delete加insert的结合。一个更有效的措施是我们可以直接把ripple从source移动到dst,而不需要放到最后
对于第一个partition来说,也就是删除的那个partition,我们需要访问两个block(最后一个和删除的那个)
假设现在的一个update操作会把一个在block i中的值删除,然后插入到block j中。首先需要做一次点查询。然后一次删除,把新出现的empty hole移动到分区的最后一个。代价则是
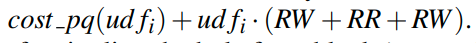
即先删除,然后读最后一个元素,然后写入到hole中(为什么不盲写呢?)
然后我们要考虑把empty hole移动到block j中。他们之间的分区数是Pi + ... Pj-1,也就是trail_parts(i) - trail_parts(j)
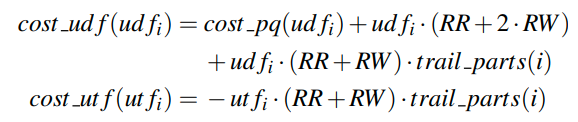
这里就是从左到右的代价。开始点需要一次点查询,然后移动hole。然后我们需要移动若干个分区到j中,最后一次插入(其实这里多统计了一个读,因为最后的分区就是j所在的分区,他其实只需要一次写入就可以,不需要读)
对于反过来的方向,操作则是一样的
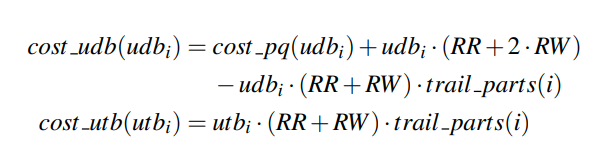

最后把他们拆开看,最后的开销取决于FrequencyModel和PartitionStrategy,分别是(fixed_term, bck_term, fwd_term, parts_term)以及(bck_read(i), fwd_read(i), trail_parts(i))。也就是说我们的cost function是由access pattern和分区策略共同决定的(而access pattern由workload和data distribution共同决定)
Cost Model Verification
每次部署的时候,我们需要确定有关读写的参数。我们通过一个micro-benchmarking来确定这些参数。并且通过插入和单点读操作就可以足够确定这些参数了。因为他们包含着模型中主要的两个代价函数:(1)后续的分区数,(2)每个分区的大小

在micro-benchmark中有若干个partition,并且分区的大小随指数增长(我好奇为什么insert在后面的partition开销这么大呢?我们应该只需要一次写才对)
这里显示了实际的开销和模型给出的结果的图,可以看出预估的效果
具体的操作应该就是线性回归,让model去拟合真实值
他原文中也说了cost和trailing partition有线性关系,但是这里为什么ID越大延迟越高呢?可能是ID越大越靠前?
Considering Ghost Values
最后需要考虑Ghost value了
ghost value就是没有被移动到最后面的empty slot,他是对于memory utilization和data movement的trade off
对于每次的插入和更新,ghost value可以避免使用ripple来获得empty slot
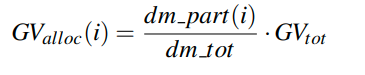
ghost value有一个总体的数量(意思是一个chunk共用一堆ghost value)
这里的dm_part就表示第i个block中的insert和update引起的ripple(不算delete的目的可能是因为当用了ghost value后,delete就不会引起ripple了?)
然后我们根据权重来分配ghost value的slot。具体的实现的话,应该就是只有分区内部才考虑ghost value,其他分区应该不会向这个分区要ghost value(否则决策点就太多了),相当于给这个分区一些弹性,让他可以处理更新的操作
Optimal Column Layout
他这里说了Pn-1是固定为1的,那可能前面有些地方的推断是错的
和上面说的一样,最后就转化成了一个优化问题,我们需要找到最优的分区位置

由于之前的式子中,有P之间的乘积,无法通过线性的求解器来求解,因为引入了高次项。所以这里用新的项替换了之前的连乘,并通过加入约束来保证他和之前的项表达的是一致的。
而这里y就表示的是连乘,他的取值范围仍然是0和1,含义大概是从j到i - 1有没有分区。
他还给出了上面提到的SLA

保证更新不超过一定的延迟
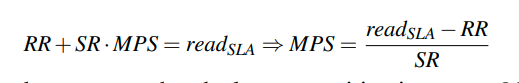
保证读不超过一定的延迟。MPS表示的是最大的分区大小。也就是保证每过MPS个block,最小有一个1
文章评论