A Comparison of Adaptive Radix Trees and Hash Tables

Abstract

比较ART, Judy Array, 两种基于二次探测哈希的变体，三种Cuckoo Hashing的变体

结果发现ART和Judy都不能与哈希方法相比

Introduction

这里提到了这里的比较只用于integer:
We only focus on keys from an integer domain. In this regard, we would like to point out that the story could change if keys were arbitrary strings of variable size

文章中提到了一个概念covering index/non-covering index（即索引内部是否存储了所有需要查询的key）

以及提到了Hashing approach中，hashing scheme和hash function都很重要（比如hash function可以决定我们的冲突等。而hash scheme决定怎么解决冲突，常用的链式方法就会导致比较差的局部性）

Radix Trees

ART是一种trie树的变体。trie树的缺点就是局部性不好，并且很耗内存。因为很多的分支都是稀疏的

trie树的优点：
1. 形状只取决于键的空间以及长度
2. 不需要rebalancing
3. 有序，支持高效的前缀查找
4. 允许前缀压缩（叶节点可以只存储后面的部分）

Judy Array根据键的分布以及数据的基数来变化他的节点的表示。从而防止了过高的内存占用以及低局部性的问题

ARTful index，也就是ART和Judy非常像，但是他没有像Judy那样设计为关联数组（比如map，这里说的应该是外层接口），而是针对主存数据库的索引设计的

Judy

1. Judy1： A bit array that maps integer keys to true or false and hence can be used as a set
2. JudyL: An array that maps integer keys to integer values(or pointers) and hence can be used as an integer to integer map
3. JudySL: An array that maps string keys of arbitrary length to integer values(or pointers) and hence can be used as a map from byte sequences to integers

为了对比后面就关注JudyL

Judy的作者发现cache miss对数据结构的影响是巨大的。我们希望避免cache-line fill（which can result in cache misses）。而Radix tree的最大缓冲行填充数取决于radix tree的高度的（每次访问都引起一次cache miss）。对于每一层来说，我们希望只访问一次cache line，并且里面保存了指针指向我们接下来要去的地方

Judy使用了很多压缩技术来避免缓存未命中。大概可以分为两类，Horizontal compression和Vertical compression

Horizontal Compression：这个技术是用来解决大个节点分散稀疏的问题的。Judy使用动态变化的节点大小。但是这时候节点就不能直接寻址了，我们需要通过比较才能知道节点具体在那里。Judy使用两种节点来解决这个问题

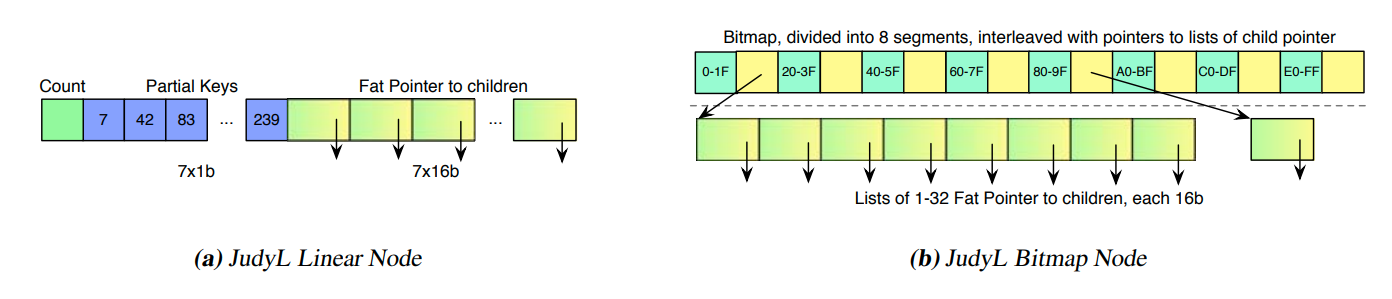
linear node就是先存储了对应的键，然后再是值

而bitmap node则是把对应的位和指针交错分布。256的值域会被用8个32位的整数划分开。注意这会导致两次cache line miss

Judy把节点的元信息存储在指针上，所以每个指针有16位，8位的物理指针，还有8位存储元数据

Vertical Compression：当节点只有一个孩子的时候，我们可以跨越这个节点。也就是skipping levels。这时候缺失的节点的key会被存储到之前提到的元数据中，用来后续的比较。这个技术又被称为path compression

另一个技术叫immediate indexing。当后面的一系列节点没有分支的时候，我们可以直接把叶子节点的值存到上面指针的位置。从而可以快速到达叶节点。我感觉这个也是用来解决分散稀疏的问题的。

ART

ART和Judy有很多类似的地方。他也是256-radix tree。使用了(1) different node types for horizontal compression, and (2) vertical compression also via path compression and immediate indexing

而这里还有两个主要的区别。第一，ART中的元数据存储在header中。他有4种类型的节点，Node4,Node16,Node48以及未压缩的Node256。ART利用了SIMD的技术来加速查找（这个比较nb，但是还是有cache的问题）。第二，ART被设计为是数据库的索引，而Judy则是通用的关联数组（kv storage）。ART不需要保存完整的键值对，而是存储一个指向table的指针即可。所以ART主要用于non-covering index。

ART中的Node4和Node16与Judy中的Linear Node相似

Node48由256字节大小的数组，以及48个子节点指针组成。这里相当于只是把pointer压缩了一下。那为什么不设计类似的Node128什么的呢？

Judy的bitmap节点弥补了大节点和小节点的gap，因为他是动态变化的（这么看来感觉bitmap的设计更好一些，但是bitmap插入可能需要重新分配内存？这样会导致大量的cache line miss）

Hash Tables

Quadratic probing

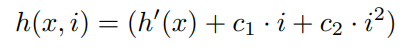
i表示的是第i次探测。二次探测的优势就是（1）容易实现（2）在哈希表的大小是2的整数次幂的时候，他可以保证每个slot都被使用到（不会出现空缺）

但是二次探测的缺点就是如果两个键在第一次探测出现了冲突。那么后面就会一直冲突。所以选择一个好的哈希函数是很关键的。（leveldb的那个bloom filter也会这样）

当table变大的时候，空间利用率低，但是效率高。而table小的时候效率低，但是空间利用率高

Cuckoo Hashing

两个哈希表T0,T1,每一个都有他自己的哈希函数h0,h1。

每一个元素要么插入到T0[h0(x)]，要么插入到T1[h1(x)]

当一个元素插入的时候，他首先探测T0，如果已经有元素y了，那么他会把y踢走，自己存到这个位置上。然后y就会去探测T1[h1(y)]。如果还是有其他元素了，y就会把那个人踢走，自己存到T1中。我们会不断循环，直到所有人都找到他的位置

但是这样可能会导致无限循环。比如当y把z从T1踢出来的时候，z需要从T0找位置。但是z之所以在T1就是因为T0有人占了他的位置。我们通过循环固定的次数来解决这个问题。当出现循环的时候，我们就会进行rehashing，选择两个新的哈希函数，然后把table中的所有函数都重新hash一遍。（这样的话rehash的时候会导致performance的问题）

当load factor小于50%的时候，cuckoo hashing才能有好的performance。但是我们可以增加table的数量，当有4个表的时候，load factor可以增加到96%，但是代价就是效率降低。

一个优化就是让一个slot里面不是只能存一个元素，而是让slot和cache line对齐

当table多的时候空间利用率高，但是效率会很低。table只有两个的时候效率高，但是空间利用率低

cuckoo hashing的好处就是我们查询的次数与load factor无关。最多只有两次。但是缺点就是对于哈希函数很敏感。

Hash functions

Multiplicative hashing:

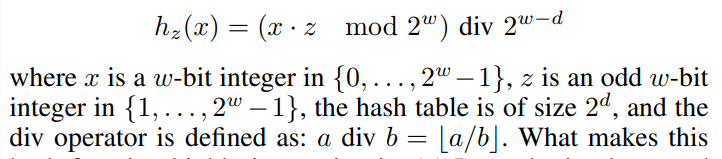
这个哈希函数是非常快的。我们可以在乘法之前就mod 2的w次幂，并且除法可以简单的通过右移来实现。并且他还有理论保证，两个数的冲突率是：

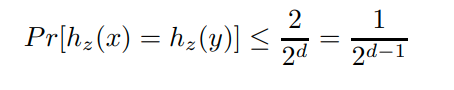
这个冲突率是理想的冲突率的2倍（应该算是非常小的了）

虽然Murmur hash相当robust，但是会带来巨大的performance degradation。我们认为multiplicative hashing是足够robust的，并且有很好的performance