这篇论文讲的就是lamport的logic lock

The Partial Ordering

如果一个事件A发生早于B，大多数人会说A发生在B之前。因为他们会用物理时间来证明这个定义。然而，如果一个系统要满足规范，那么这个规范就必须根据系统内可观察到的事件给出。如果我们的规格是物理时间，那么系统必须包含真正的时钟，而且就算是他包含了真正的时钟，我们也会遇到时钟不准确的可能性。所以我们不通过物理时钟定义“happened before“

我们假设一个系统由若干个进程组成，每个进程包含了具有全序关系的若干个事件。同时将进程间的发送消息和接受消息也定义为事件

我们让->表示happend before，然后有如下的定义：
1. 如果a和b是在同一个进程中的事件，并且a在b的前面，则a->b
2. 如果a是一个进程发送一个消息，而b是另一个进程接收这个消息，那么a->b
3. 如果a->b,b->c，则a->c

对于两个事件，如果不满足a->b，也不满足b->a，那么说a和b是并发的

同时也假设不存在a->a这种情况。所以综上可以发现->是一个自反的偏序关系

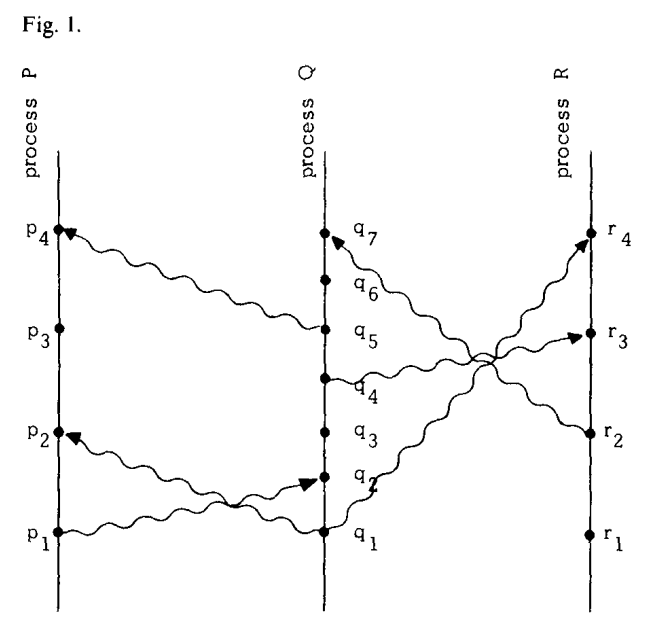
图中是一个演示，其中点表示了事件，而曲线表示的是消息的发送。通过图可以看出如果a->b，那么我们可以沿着进程线以及消息线按照时间增加的方向从a移动到b

另一种看待这个定义的方式是说如果a->b，那么就有可能a对b有因果影响(casually affect)，如果两个事件没有因果关系，那么两个事件就是并发的

后面他提到了这个定义和狭义相对论的近似。但是狭义相对论中的事件指的是"messages that could be send"，而我们的系统中则是"messages that actually are send"

Logical Clocks

我们定义系统中的clock。对于Ci来说，他就是进程Pi对应的时钟。那么Ci\langle a \rangle则代表了对应进程中的事件a的时间。而对于整个系统的始终C以及任意的事件b来说，则有C\langle b \rangle = Cj\langle b \rangle

结合之前的符号->，我们可以给出一个定义，对于任意的事件a，b，如果a->b，则C\langle a \rangle

注意对于反过来的情况是不成立的，因为他们可能是并发的关系，而非happen before

然后再根据->符号的定义，我们可以得到两个条件：
* C1: If a and b are events in process Pi, and a comes before b, then C_i \langle a \rangle
* C2: If a is the sending of a message by process Pi and b is the receipt of that message by process Pj, then C_i \langle a \rangle

然后将clock加入到之前的figure 1中

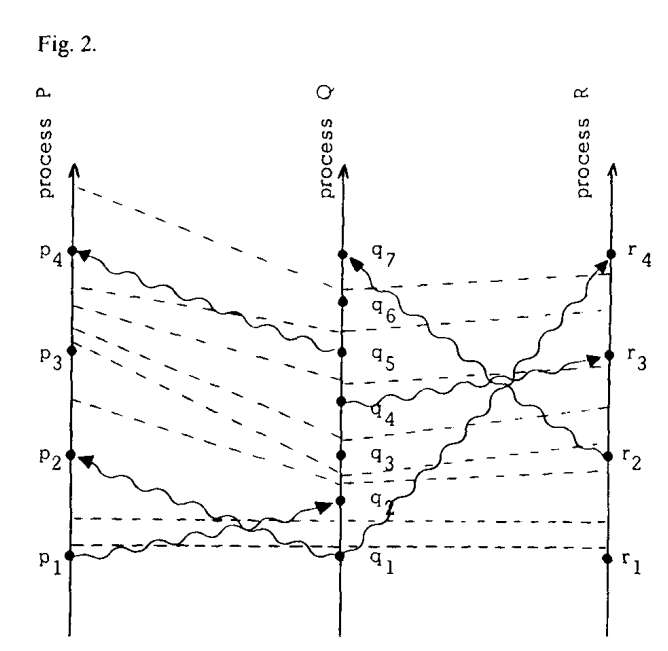
图中的虚线代表了tick line，即每次clock tick

C1指定了，同一个进程线下的每两个事件之间都必须有一次tick

而C2指定了对于每一条message line，都必须穿过一个tick line

我们可以将tick line作为时间轴上的坐标线（我不知道咋翻译了，含义就是平行于时间轴的线），然后重新画出figure 2

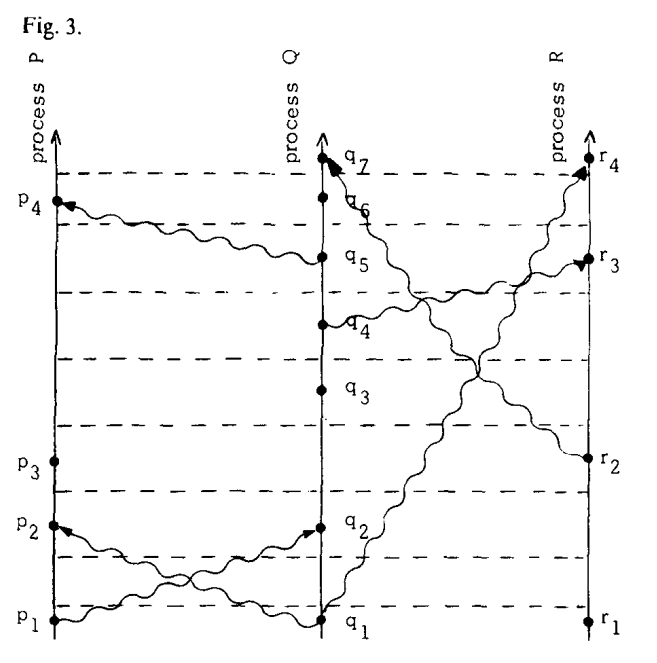
现在假设Ci是进程Pi的时钟寄存器，即当事件a发生的时候，Ci的值是C_i \langle a \rangle，然后下面说我们怎么实现上面提到的clock

对于C1条件来说，我们有：
IR1：Each process Pi increments Ci between any two successive events.

对于C2来说，我们要求每个信息m都要包含他的timestamp Tm，也就是发送消息时候的时间。而进程则必须将其时钟调整到大于Tm。具体的：
IR2(a): If event a is the sending of a message m by process Pi, then the message m contains a timestamp Tm = C_i\langle a \rangle. (b): Upon receiving a message m, process Pj sets Cj greater than or equal to it's present value and greater than Tm.

通过这两个规则，我们就可以让我们的clock满足上面的条件，也就可以追踪到因果关系

Ordering the Events Totally

对于构造全序关系，我们可以结合用任意的一个进程间的全序关系即可。如果两个事件发生的时间相同，那么就用进程之间的全序关系导出事件的全序关系即可。

然后论文中给出了一个通过全序关系解决问题的例子

核心就是通过在消息之间传递时间戳，从而传递因果关系。即如果一个进程收到了其他进程的确认信息，那么就可以保证该进程已经知道了所有在他之前的请求。

这里的因果有两点，如果进程i确认了进程j的请求，那么进程j后续的请求一定会排在进程i现有请求的后面。如果进程i收到了进程j的请求，那么进程i后续的请求一定会排在进程j现有请求的后面。

这样我们就可以构造出两个进程的请求的前后顺序，从而防止出现因果颠倒的情况。

Anomalous Behavior

这里讲的就是对于系统检测不到的因果关系，我们是没办法去构造一个预期的顺序的。

第一种解决的方法就是人工来去指定涉及到外部消息时候的timestamp。

而第二种方法则是构造一个新的系统，满足Strong Clock Condition，即可以探测到外部事件的情况。而很棒的一点是，我们是有可能通过相互独立的物理时钟来构造这样的系统的。所以我们可以通过物理时钟来消除掉这些异常现象。

Physical Clocks

我们在之前的时空图下引入物理时间轴，然后令C_i(t)代表在物理时间t下读取Ci的值。为了数学方面的方便，我们假设时钟是连续的，而非是在离散的tick中运行的

更准确的说，我们可以假设C_i(t)是一个连续可微的函数，那么对应的导数就代表了时钟增加的速率

为了确保时钟Ci是一个物理时钟，我们需要确保他在近似正确的速率上运行，即dC_i(t) / dt \approx 1

更具体的，我们这样假设:
PC1. There exists a constant \kappa << 1, such that for all i: |dC_i(t)/dt - 1|<\kappa

对于ctystal controlled clocks，\kappa \leq 10^{-6}

每一个clock都独立的运行在正确的速率上还不够，我们还需要保证他们是同步的，即：
PC2. For all i,j: | C_i(t) - C_j(t) |<\epsilon

对于figure2来说，如果我们假设tick line代表了物理时间，那么一个tick line在高度上的变化就不能超过\epsilon

现在我们考虑，我们需要多小的\kappa以及\epsilon才能保证不会出现之前提到的异常现象

我们首先假设我们的时钟已经满足了之前的要求，即在不出现系统外部的消息的情况下，我们可以保证顺序。现在只需要考虑的情况就是当用之前的规则错误的时候，我们怎么通过物理时钟来保证不会出现这种情况

我们假设当出现a \boldsymbol{\rightarrow} b(即Strong Clock Condition的条件下)的时候，满足a发生在t时刻，而b发生在t + \mu时刻后。换句话说就是\mu是进程间通信的最小的时间

为了防止异常情况的发生，我们需要保证C_i(t + \mu) - C_j(t) > 0。然后把这条规则和上面的PC1以及PC2结合到一起，就可以得到一个关系。注意我们假设当clock重置的时候，我们不会让时钟回调（因为要保证C1的成立）

PC1则指出C_i(t + \mu) - C_i(t) > (1 - \kappa)\mu
然后根据PC2可以推导出当\epsilon/(1 - \kappa) \leq \mu的时候满足 C_i(t + \mu) - C_j(t) > 0

然后说一下怎么保证PC2的条件，因为时钟会偏移，所以随着时间流逝他们会偏移的越来越多

m代表一个消息，从物理时间t发送，并在物理时间t`接收。我们定义vm = t` - t，作为消息m的总延迟。这个延迟对于收到消息的进程来说是感知不到的。我们可以假设一个最小延迟\mu_m \geq 0，并且\mu_m \leq v_m。我们称\xi_m = v_m - \mu_m为不可预测的延迟(unpredictable delay)

我们现在为物理时钟定义一些规则：
IR1`： For each i, if Pi does not receive a message at physical time t, then Ci is differentiable at t and dC_i(t) / dt > 0
IR2`: (a) If Pi sends a message m at physical time t, then m contains a timestamp T_m = C_i(t). (b) Upon receiving a message m at time t`, process Pj sets Cj(t`) equal to maximum(Cj(t` - 0), Tm + \mu_m)

现在考虑进程之间的关系为一个图，如果Pi到Pj有一条弧，则有一条消息会在每\tau秒从Pi向Pj发送一条消息。图的直径d则是对于图中的任意两个点，他们的之间最多有d条弧

假设任意一个强连通的图都可以满足IR1`以及IR2`。假设对于任意的消息m，有\mu_m \leq \mu，以及对于所有的t \geq t_0，则有(a) PC1 holds. (b) There are constants \tau and \xi such that every \tau seconds a message with an unpredictable delay less thant \xi is send over every arc. Then PC2 is satisfied with \epsilon \approx d(2\kappa\tau + \xi) for all t \gtrsim t_0 + \tau d, where the approximations assume \mu + \xi \ll \tau