通过SARSA和QLearning来理解一下on policy和off policy
1. Q-learning（Off-policy）
- 更新公式：
Q(s,a) \leftarrow Q(s,a) + \alpha \Big( r + \gamma \max_{a'} Q(s',a') - Q(s,a)\Big)
- Q-learning 在更新时，使用的是 下一状态 s' 中的最大动作价值 \max_{a'} Q(s',a')，即假设下一步总是采取最优动作。
- 这意味着它学习的是 最优策略（greedy policy），而不管实际执行过程中你是用 ε-greedy、softmax，还是完全随机策略。
- 所以即使训练时用旧策略（探索多、次优动作多），也不妨碍学习到最优 Q^*。这就是 off-policy：学习目标策略（最优）与实际行为策略（探索）可以不同。
2. SARSA（On-policy）
-
更新公式：
Q(s,a) \leftarrow Q(s,a) + \alpha \Big( r + \gamma Q(s',a') - Q(s,a)\Big)
- SARSA 在更新时，使用的是 实际选择的下一步动作 a' 的价值，而不是最大值。
- 它学习的是 当前执行的策略本身（如 ε-greedy 策略）。
- 如果你在训练时不用当前策略，而用旧的策略去更新，得到的值函数就和实际执行的策略不匹配，更新就会失真。
- 因为它是 on-policy：必须保证学习的策略和实际行为策略一致。
SARSA的全称是(state, action, reward, state, action)，也就对应了用来更新Q table的五元组(s, a, r, s', a')
然而用这个五元组做训练的时候，是不能使用经验回放的，因为SARSA是on policy的。但是看到这里可能会有一个直观的想法，这单独的一个五元组其实是和策略无关的，为什么和on/off policy有关呢
因为我们在训练的时候，无法直接计算这里贝尔曼方程中的期望，所以通过采样的方式来做近似。
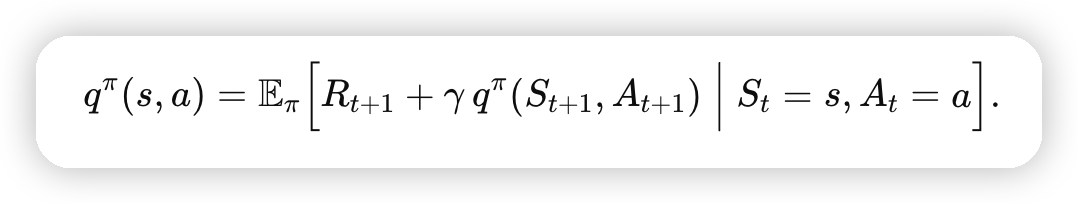而采样的五元组是依赖策略的，所以不能随便更换策略，否则采样出来计算的q就不是针对这个策略的q了
而Q learning是学习的最优Q函数，和策略是无关的，而和reward/状态转移，这两个随机变量相关。可以理解为是通过训练数据学习“环境”的最优Q函数。
文章评论