初探

• 强化学习用智能体（agent）这个概念来表示做决策的机器。相比于有监督学习中的“模型”，强化学习中的“智能体”强调机器不但可以感知周围的环境信息，还可以通过做决策来直接改变这个环境，而不只是给出一些预测信号。

• 面向决策任务的强化学习和面向预测任务的有监督学习在形式上是有不少区别的。首先，决策任务往往涉及多轮交互，即序贯决策；而预测任务总是单轮的独立任务。如果决策也是单轮的，那么它可以转化为“判别最优动作”的预测任务。其次，因为决策任务是多轮的，智能体就需要在每轮做决策时考虑未来环境相应的改变，所以当前轮带来最大奖励反馈的动作，在长期来看并不一定是最优的。

• 强化学习和有监督学习的学习目标其实是一致的，即在某个数据分布下优化一个分数值的期望。不过，经过后面的分析我们会发现，强化学习和有监督学习的优化途径是不同的。

  • 整个交互过程的每一轮获得的奖励信号可以进行累加，形成智能体的整体回报（return），好比一盘游戏最后的分数值。
  • 通过累加等方式计算多轮共同的得分？或者是计算最后一步状态的得分。
• 有监督学习和强化学习的区别。
  • 有监督学习的任务建立在从给定的数据分布中采样得到的训练数据集上，通过优化在训练数据集中设定的目标函数（如最小化预测误差）来找到模型的最优参数。这里，训练数据集背后的数据分布是完全不变的。
  • 具体而言，强化学习中有一个关于数据分布的概念，叫作占用度量（occupancy measure），归一化的占用度量用于衡量在一个智能体决策与一个动态环境的交互过程中，采样到一个具体的状态动作对（state-action pair）的概率分布。
    • 这里理解成是模型决策的分布吗？即给定一个state，采取对应action的概率
  • 占用度量有一个很重要的性质：给定两个策略及其与一个动态环境交互得到的两个占用度量，那么当且仅当这两个占用度量相同时，这两个策略相同
    • 即占用度量用来表示模型的策略
  • 强化学习的策略在训练中会不断更新，其对应的数据分布（即占用度量）也会相应地改变。因此，强化学习的一大难点就在于，智能体看到的数据分布是随着智能体的学习而不断发生改变的。
    • 这句话好像在说占用度量并不是策略。根本意思更像是在说明策略改变后，看到的状态也有变化。

* 有监督学习，学习的是函数/模型，数据分布不变，输入到模型中，输出结果。目的是优化这个输出结果
* 这里提到的强化学习是修改数据分布而目标函数不变

多臂老虎机

探索与利用是与环境做交互学习的重要问题，是强化学习试错法中的必备技术，而多臂老虎机问题是研究探索与利用技术理论的最佳环境。了解多臂老虎机的探索与利用问题，对接下来我们学习强化学习环境探索有很重要的帮助。对于多臂老虎机各种算法的累积懊悔理论分析，有兴趣的同学可以自行查阅相关资料。 -贪婪算法、上置信界算法和汤普森采样算法在多臂老虎机问题中十分常用，其中上置信界算法和汤普森采样方法均能保证对数的渐进最优累积懊悔。

多臂老虎机问题与强化学习的一大区别在于其与环境的交互并不会改变环境，即多臂老虎机的每次交互的结果和以往的动作无关，所以可看作无状态的强化学习（stateless reinforcement learning）。第 3 章将开始在有状态的环境下讨论强化学习，即马尔可夫决策过程。

大概理解到是根据不等式预估上界去选择就行

记录每个杆的奖励，根据这个对每个动作的奖励分布进行建模。再在此之上进行采样。
感觉像是在上面贪心的基础上，做了个采样，而不是每次选期望最大的。因为这样可能导致错过一些机会。

马尔可夫决策过程

* 更像是没有动量

动态规划

* 根据当前策略，评估当前状态。然后根据当前的状态，选择最优的action，生成新的策略，直到收敛

这两种算法都是生成一个确定的策略（在某一个state下，选择一个确定的action），用的是贪心的方法。

时序差分算法

另一个地方gemini老师给讲了

核心点：一个状态的真实价值，等于采取一个动作后得到的即时奖励与下一个状态的折扣价值的期望

Sarsa算法

用上面相同的方式，来预估动作价值函数

然后和上面的动态规划类似可以取最优。

不过这里我理解的一个区别可能是（口糊的），动态规划因为已经有全部的状态了，所以应该是可以计算出最终的结果的，这里model free的情况下，可能会陷入局部最优。所以可以不用每次取最优，而是以一个概率随机选择一个动作。

class Sarsa:
    """ Sarsa算法 """
    def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])  # 初始化Q(s,a)表格
        self.n_action = n_action  # 动作个数
        self.alpha = alpha  # 学习率
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略中的参数

    def take_action(self, state):  # 选取下一步的操作,具体实现为epsilon-贪婪
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action

    def best_action(self, state):  # 用于打印策略
        Q_max = np.max(self.Q_table[state])
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):  # 若两个动作的价值一样,都会记录下来
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a

    def update(self, s0, a0, r, s1, a1):
        td_error = r + self.gamma * self.Q_table[s1, a1] - self.Q_table[s0, a0]
        self.Q_table[s0, a0] += self.alpha * td_error

代码实现上就比较清楚，选择动作的时候，有一定概率从Q table中选最优的。然后每次选完更新一下预估的动作价值函数。

多步Sarsa

1. 偏差 (Bias)

• 定义： 偏差是指你的估算值与真实值之间的系统性差异。如果一个估计器是有偏的，意味着它会系统性地高估或低估真实值。
• 在强化学习中的体现：
  • 蒙特卡洛（Monte Carlo, MC）方法： 这些方法通常被认为是无偏的。因为它们通过完整的奖励序列（从当前状态到回合结束）来计算回报，直接使用实际的奖励总和来更新价值，所以它们趋向于平均而言得到真实值。
  • 单步时序差分（TD）方法（如基础Sarsa）： 这些方法通常是有偏的。它们使用“自举”（bootstrapping）的方式，即用当前已有的对未来状态的估算值来更新当前的价值。由于这些未来状态的估算值本身可能不准确（因为它们也是估计），因此会引入偏差。

2. 方差 (Variance)

• 定义： 方差衡量的是估算值围绕其平均值的波动程度或不稳定性。高方差意味着你的估算值在不同的采样或运行中会发生很大的变化。
• 在强化学习中的体现：
  • 蒙特卡洛（MC）方法： 它们通常具有高方差。因为每次回合的轨迹都是随机的，不同的动作选择和环境反馈会导致非常不同的奖励序列，从而使得最终的回报值波动很大。
  • 单步时序差分（TD）方法： 它们通常具有低方差。因为它们只向前看一步，并且主要依赖于下一状态的估计值，这使得更新更平滑，受单个随机事件的影响较小。

3. 多步Sarsa算法中的权衡

多步Sarsa算法（例如n步Sarsa）就是为了在偏差和方差之间找到一个平衡点。

• 它介于单步TD方法和蒙特卡洛方法之间。
• 如何平衡： 多步Sarsa通过向前看n步来收集实际的奖励，然后再从第n+1步的状态开始进行自举。
  • 通过纳入n步的实际奖励，它减少了单步TD方法的偏差，因为目标值更接近真实的回报。
  • 通过在n步后进行自举，它减少了蒙特卡洛方法的高方差，因为它不需要等待整个回合结束才进行更新，从而降低了对长序列随机性的依赖。

因此，多步Sarsa算法的参数n（或一些算法中的σ参数）允许你控制这种权衡：
* n较小（接近1）： 结果更接近单步Sarsa，具有较高偏差和较低方差。
* n较大（接近回合长度）： 结果更接近蒙特卡洛方法，具有较低偏差和较高方差。

选择合适的n值，通常可以在学习速度和最终性能之间获得更好的平衡。

直观理解就是往后多看几步再来确定当前的决策是否正确。
* 比如n=1的时候，如果一个action的价值比较大，那选择了以后会直接增加这个Q(s, a)的值
* 但是假如移动过去的状态并不好，可能后续的状态价值都很低，那么其实上面预估的Q(s, a)应该就比较低。核心点在于只看了一步，没有往后多看，就用当前的预估值来更新了。
* 所以结合蒙特卡洛方法，往后多走几步，就可以更好的知道这个状态的价值预估了

Q-learning

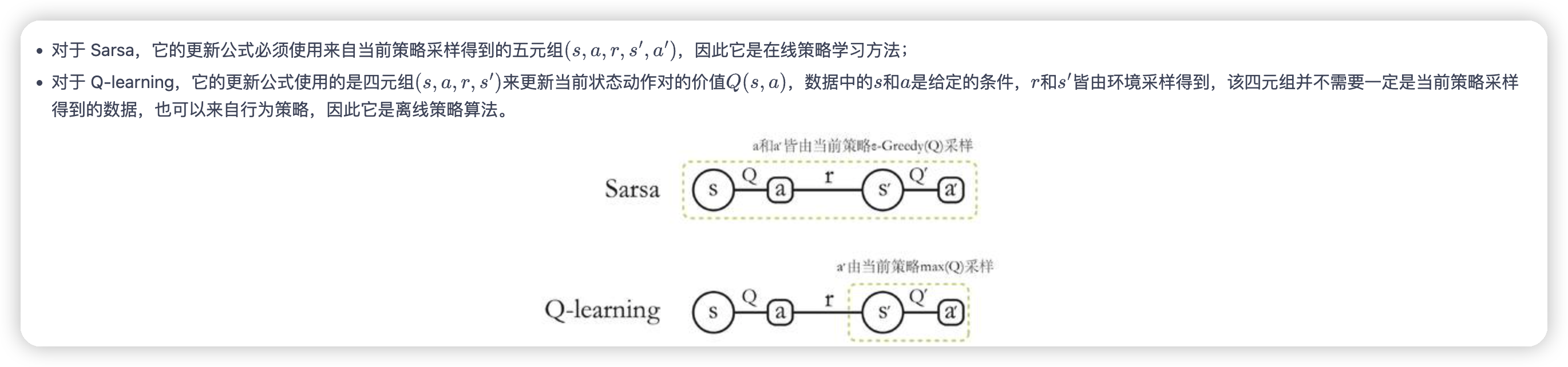
* sarsa的更新公式需要在下一个state执行一下策略，得到next_action，然后才能更新当前状态的价值预估
* Q learning的更新公式则是取下一个state的max值来获取，而不依赖当前的策略

Dyna-Q

直观理解就是在执行的过程中用历史交互的数据来建模环境。

这个M(s, a)就是预估的对环境的建模。然后每次会通过Q planning，也就是使用对环境的建模来模拟一批数据出来，用来优化Q。

这里公式中学习模型这一步是确定的，应该通过一些其他公式可以建模一些不确定的环境，直观想就是把历史的序列放进去直接sample。取决于对环境的先验知识了