Daily C/C++ 三分法

三分法

三分法其实是比较常见的一个方法了，也是比较基础的一个算法

和我们常听到的二分法不同，二分法是在满足单调性的区间上去查找值，而三分法是用来求解单峰函数的极值的

正好今天的leetcode每日一题是一个求解单峰极值的问题，这里我们就用三分法来解决他

题目链接

就像是他的名字一样，三分法要求我们将区间分成三段，也就是找到两个端点

这里我们看对于一个单峰图像进行三分的结果

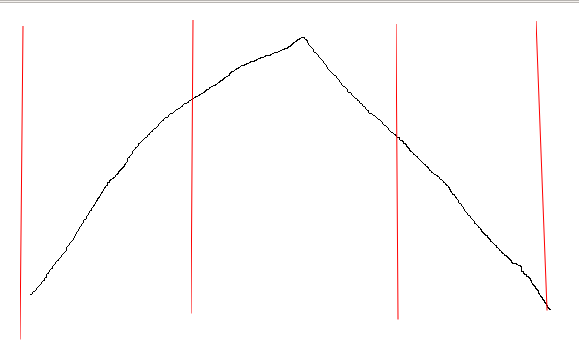
比较简陋，两边的红线就是我们的两个端点，中间的两个红线就是我们三分出来的端点

我们可以通过很简单的mid1 = left + (right - left) / 3 和 mid2 = right - (right - left) / 3 来得到这两个端点

接下来就是要考虑两个端点的关系，然后根据结果我们决定下一步要怎么缩小区间

其实在这里我们可以这样考虑，对于三分法来说，如果是一个点高我们就选择这个点的话，那么我们可能就会陷入局部最优的情况。因为我们是有两个方向逼近这个高点的，所以就导致我们无法判断到底是让高点和那边的端点构成新的区间。

但是，如果考虑淘汰，如果一个端点是低点的话，那我们可以无需考虑的将其抛弃。因为我们是单峰函数，两边低中间高，所以如果是mid1低，我们就抛弃左边的区间，否则就抛弃右边的区间。

这样一步一步的缩小区间，最终就可以得到正确的结果。

模板如下

while (lb < ub) {
    mid1 = lb + (ub - lb) / 3;
    mid2 = ub - (ub - lb) / 3;
    if (f(mid1) < f(mid2))
        lb = mid1;
    else 
        ub = mid2;
}

其实对于不同的数据类型，也有小差异在里面，比如比较double要加上一个eps。 但是主体的思路是不变的

这里最后贴上leetcode题的代码方便大家理解

int lb = 0, ub = arr.size() - 1;
while (lb < ub) {
    int mid1 = lb + (ub - lb) / 3;
    int mid2 = ub - (ub - lb) / 3;
    if (arr[mid1] < arr[mid2]) {
        lb = mid1 + 1;
    } else {
        ub = mid2 - 1;
    }
}
return ub;

还要说上一句的就是，对于下标的三分，因为下标是离散的原因，我们无法很好的取到端点的值。

所以这里的解决方法就是自己主动的进行区间的偏移，而正确性是不变的。因为低点本身就是低于高点的值，我们是闭区间，所以去掉低点本身是没有问题的。

同时最后考虑边界条件，两个值相差一的时候，低点和高点就是两个端点。无论那个值改变都会使最终区间重合，得到答案，而不是进入死循环。