读一下知乎这篇文章:https://zhuanlan.zhihu.com/p/456863215
在GPT2中,对layer normalization做了优化
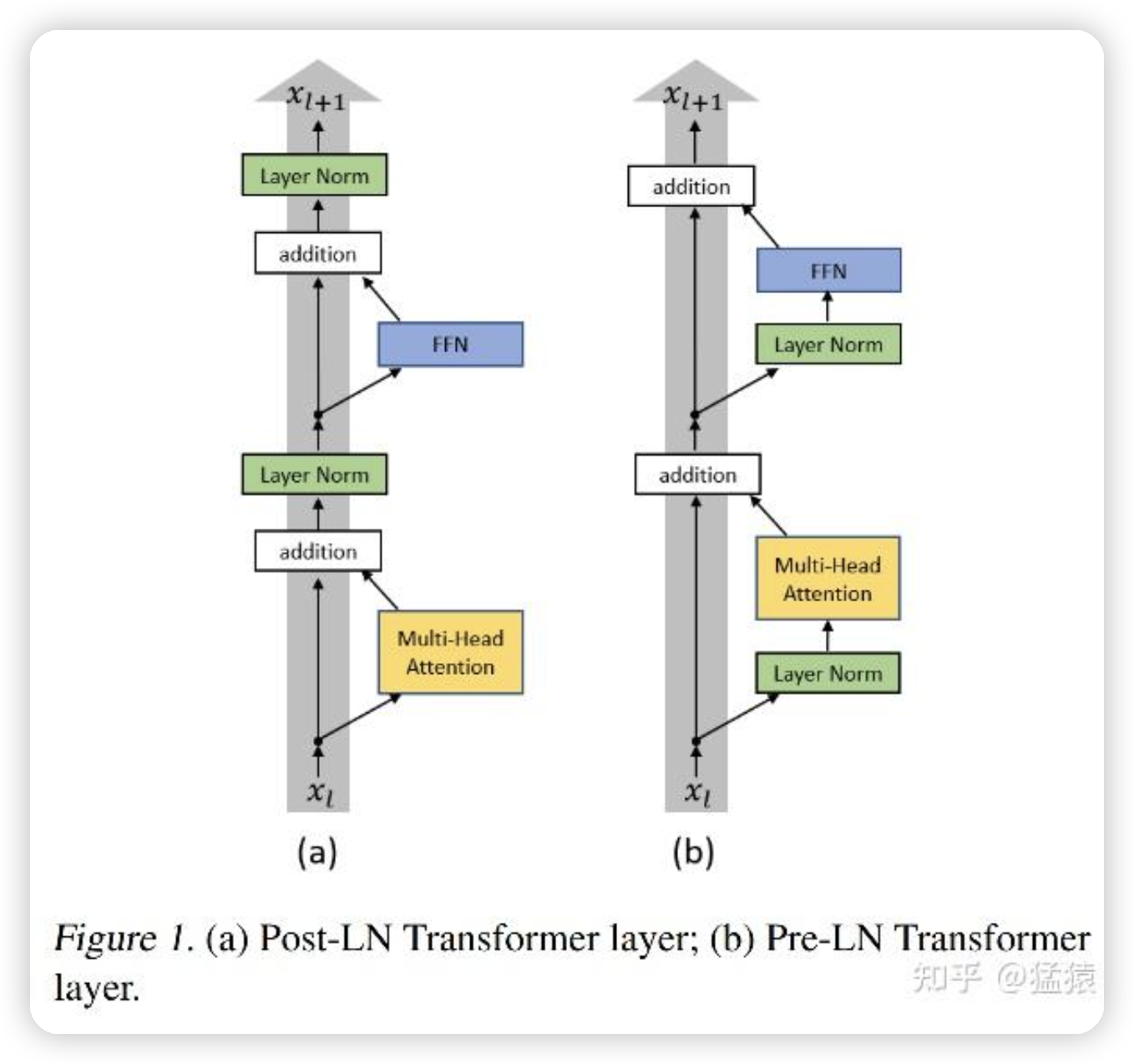
把layer norm从残差层后面放到了残差层内部。
总结看来,Pre-LN带来的好处,基本都是因为不需要做warm-up引起的。而引起这一差异的根本原因是:
- Post-LN在输出层的gradient norm较大,且越往下层走,gradient norm呈现下降趋势。这种情况下,在训练初期若采用一个较大的学习率,容易引起模型的震荡。
- Pre-LN在输出层的gradient norm较小,且其不随层数递增或递减而变动,保持稳定。
- 无论使用何种Optimzer,不采用warm-up的Post-LN的效果都不如采用warm-up的情况,也不如Pre-LN。
这里deepseek帮忙细节解释了一下:
在深度学习中,Gradient Norm(梯度范数) 指梯度向量的 L2 范数(即所有梯度分量的平方和的平方根),它衡量了梯度的大小。梯度范数过大可能引发参数更新剧烈,导致训练震荡或不收敛;梯度范数过小则可能导致参数更新停滞(梯度消失)。
为什么 Post-LN 的 Gradient Norm 不稳定?
Post-LN(后归一化) 的结构如下(以 Transformer 为例):
输出 = LayerNorm(子层输出 + 输入)
这里的“子层”可以是自注意力或前馈网络。
问题根源:
1. 梯度逐层放大
- 在反向传播时,输出层的损失梯度会直接经过 LayerNorm 的反向计算。由于 LayerNorm 在残差连接之后,输出层的梯度需要经过多个 LayerNorm 层逐层反向传播到下层。
- LayerNorm 的梯度计算中包含对输入的缩放操作(与输入方差相关),如果输入方差较大,梯度可能被放大。
- 梯度分布不均衡
- 高层(靠近输出)的 LayerNorm 直接受损失函数影响,梯度范数较大;
- 低层(靠近输入)的梯度需要经过多个 LayerNorm 的反向传播,梯度范数会因连续缩放而衰减,导致梯度范数随层数增加而递减。
- 训练初期震荡
- 如果初始学习率较大,高层的大梯度会导致参数剧烈更新,而低层的小梯度无法有效调整参数,整体训练不稳定。
为什么 Pre-LN 能解决这个问题?
Pre-LN(预归一化) 的结构如下:
输出 = 子层(LayerNorm(输入)) + 输入
关键改进:
1. 输入稳定化
- 每个子层的输入都经过 LayerNorm 归一化,确保输入分布始终稳定(均值为0,方差为1),减少了梯度对输入方差的依赖。
- 梯度传播更均衡
- 反向传播时,梯度不再需要经过多个 LayerNorm 的反向计算(因为 LayerNorm 在残差分支外)。
- 梯度可以直接通过残差路径(
+ 输入)无衰减地传递到低层,各层的梯度范数趋于一致。
- 无需 Warm-up
- 由于梯度范数稳定,训练初期即使使用较大学习率,参数更新也不会因梯度剧烈变化而震荡,因此不再需要逐步增加学习率的 Warm-up 策略。
直观对比
| 特性 | Post-LN | Pre-LN |
|---|---|---|
| 梯度范数分布 | 高层大、低层小,不稳定 | 各层接近,稳定 |
| 训练初期稳定性 | 依赖 Warm-up | 无需 Warm-up |
| 深层训练难度 | 容易梯度消失/爆炸 | 更易训练深层模型 |
| 典型应用 | 原始 Transformer | GPT-3、LLaMA 等现代模型 |
例子说明
假设一个 12 层的 Post-LN 模型:
- 第 12 层(输出层):梯度范数可能为 100(较大);
- 第 1 层(输入层):梯度范数可能衰减到 1(较小)。
而 Pre-LN 模型:
- 所有层:梯度范数保持在 10 左右,波动较小。
Post-LN 的输出层梯度远大于低层,容易导致高层参数更新过快,低层更新过慢,引发震荡。Pre-LN 的均衡梯度则避免了这一问题。
总结
Pre-LN 通过将 LayerNorm 置于残差分支内,使得梯度传播不再依赖 LayerNorm 的缩放,从而稳定了各层的梯度范数。这种结构简化了优化过程,使超大规模模型(如 GPT-3)的训练更加稳定高效。
然后一个follow-up的问题是:
为什么Pre-LN是 输出 = 子层(LayerNorm(输入)) + 输入 而不是 输出 = LayerNorm(子层(输入)) + 输入
这是一个非常关键的问题!要理解为什么 Pre-LN 的结构是 输出 = 子层(LayerNorm(输入)) + 输入 而不是 输出 = LayerNorm(子层(输入)) + 输入,我们需要从 梯度传播 和 模型稳定性 两个角度深入分析。
两种结构的直观对比
假设输入为 ( x ),子层操作(如自注意力或前馈网络)为 ( F ),两种结构如下:
- 标准 Pre-LN(正确结构)
\text{输出} = F(\text{LayerNorm}(x)) + x- LayerNorm 在子层之前:先归一化输入,再将归一化后的结果输入子层。
- 用户提出的变体(错误结构)
\text{输出} = \text{LayerNorm}(F(x)) + x- LayerNorm 在子层之后:先对原始输入 ( x ) 做子层操作,再归一化子层输出,最后与原始输入相加。
这两种结构的差异看似微小,但对梯度传播的影响截然不同。
为什么标准 Pre-LN 更优?
1. 梯度传播路径的差异
- 标准 Pre-LN:
- 梯度从损失函数反向传播时,会通过两条路径:
- 子层路径:( \nabla F(\text{LayerNorm}(x)) )
- 残差路径:直接通过 ( +x ) 传递(无变换)。
- 残差路径提供了“高速公路”,使梯度可以直接无衰减地传递到浅层,缓解梯度消失问题。
- 梯度从损失函数反向传播时,会通过两条路径:
- 变体结构:
- 梯度需要经过子层 ( F(x) ) 和 LayerNorm 的反向传播:
\nabla \text{LayerNorm}(F(x)) \cdot \nabla F(x) - LayerNorm 在子层之后:相当于在子层输出上引入额外的缩放操作,可能放大或缩小梯度,破坏残差连接的稳定性。
- 梯度需要经过子层 ( F(x) ) 和 LayerNorm 的反向传播:
2. 输入输出的稳定性
- 标准 Pre-LN:
- 子层 ( F ) 的输入是经过 LayerNorm 归一化的,保证 ( F ) 的输入分布稳定(均值为0,方差为1)。
- 子层可以专注于学习残差(即 ( F(\text{LayerNorm}(x)) ) 的幅度较小),避免参数更新剧烈。
- 变体结构:
- 子层 ( F ) 直接处理原始输入 ( x ),其输出可能具有较大的方差(尤其是深层网络中)。
- LayerNorm 虽然会对子层输出进行归一化,但子层本身的输出波动可能加剧训练不稳定性。
3. 实验验证
- 实际训练中,变体结构(LayerNorm 在子层之后)的表现通常不如标准 Pre-LN,甚至可能劣于 Post-LN。
- 论文 On Layer Normalization in the Transformer Architecture 通过实验证明:将 LayerNorm 放在残差分支内(即标准 Pre-LN)是稳定训练的关键。
深入分析:为什么不能交换 LayerNorm 和子层的位置?
场景假设
假设我们强行使用变体结构 ( \text{输出} = \text{LayerNorm}(F(x)) + x ),会发生什么?
- 梯度爆炸/消失风险
- 子层 F(x) 的输入是原始数据 ( x \(未归一化),深层网络中 ( x ) 的方差可能逐层累积,导致 F(x) 的输出方差过大。
- LayerNorm 虽然会对 ( F(x) ) 的输出进行归一化,但反向传播时,梯度需要经过 ( F(x) ) 的反向计算。如果 ( F(x) ) 的输出方差过大,其梯度可能不稳定。
- 残差连接失效
- 残差连接的核心思想是让网络更容易学习“残差”(即 ( F(x) \approx 0 ))。
- 在标准 Pre-LN 中,由于输入已被归一化,( F(\text{LayerNorm}(x))) 的幅度较小,残差连接可以有效工作。
- 在变体结构中,( F(x) ) 的幅度可能较大,导致 ( \text{LayerNorm}(F(x)) ) 与 ( x ) 的数值范围差异显著,使相加操作难以稳定。
- 与 Post-LN 的相似性问题
- 变体结构 ( \text{LayerNorm}(F(x)) + x ) 实际上接近 Post-LN 的行为(因为 LayerNorm 仍然位于主分支上)。
- 实验表明,这种结构仍然需要 Warm-up 来稳定训练,无法发挥 Pre-LN 的优势。
标准 Pre-LN 的梯度传播优势
通过一个 2 层模型 的简化例子对比两种结构:
标准 Pre-LN(稳定)
- 第 1 层输入:( x_1 = x )
- 第 1 层输出:( x_2 = F_1(\text{LayerNorm}(x_1)) + x_1 )
- 第 2 层输入:( x_2 )
- 第 2 层输出:( x_3 = F_2(\text{LayerNorm}(x_2)) + x_2 )
反向传播:
- 梯度从 ( x_3 ) 到 ( x_1 ) 时,可以通过残差路径直接传递(红色箭头),不受 LayerNorm 和子层的影响,保持梯度范数稳定。
变体结构(不稳定)
- 第 1 层输入:( x_1 = x )
- 第 1 层输出:( x_2 = \text{LayerNorm}(F_1(x_1)) + x_1 )
- 第 2 层输入:( x_2 )
- 第 2 层输出:( x_3 = \text{LayerNorm}(F_2(x_2)) + x_2 )
反向传播:
- 梯度必须经过 LayerNorm 和子层的反向计算(蓝色箭头),残差路径被 LayerNorm 阻断,梯度范数可能逐层衰减或放大。
总结
- Pre-LN 的标准结构 通过将 LayerNorm 置于残差分支内,保证了梯度可以通过残差路径无衰减传播,同时稳定子层的输入分布。
- 变体结构 破坏了残差连接的“高速公路”特性,使梯度传播重新依赖 LayerNorm 和子层的复杂变换,失去了 Pre-LN 的核心优势。
因此,Pre-LN 的设计是经过理论和实验验证的最优选择,而简单的 LayerNorm 位置调换会导致性能下降甚至训练失败。
主要是因为,如果最后走norm,那么反向传播回来的时候,就需要先通过norm的放缩,会影响梯度。同时输入给FFN的数据也不是归一化后的。
文章评论