排序

区分的主要依据就是算法是否是基于比较的

leetcode排序

算法可视化

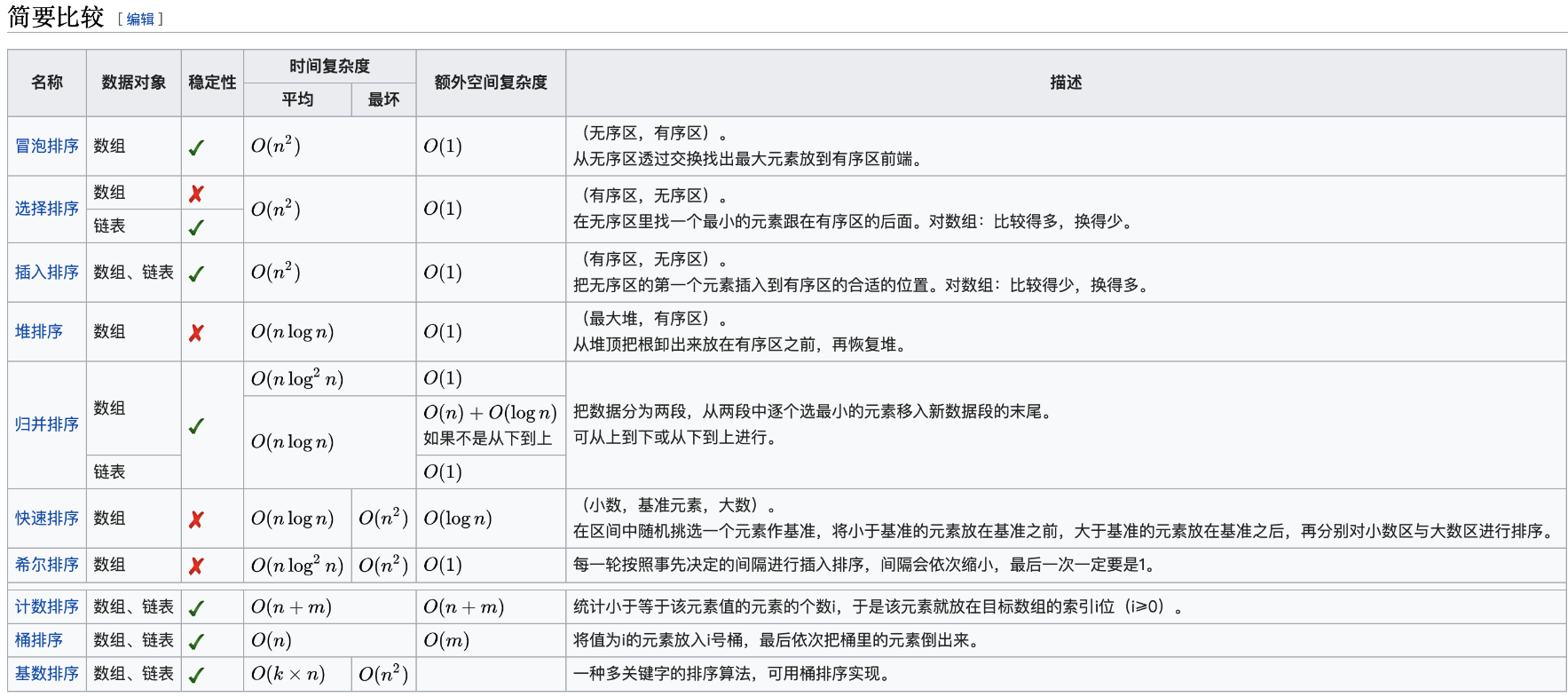
图是leetcode题解上的

这里不打算具体的说计数排序和桶排序，因为思路较为简单

代码均在leetcode上测试过，可以放心的使用

选择排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        for (int i = 0; i < n; i++) {
            int minn = i;
            for (int j = i + 1; j < n; j++) {
                if (nums[j] < nums[minn]) minn = j;
            }
            swap(nums[minn], nums[i]);
        }
        return nums;
    }
};

从后面未排序的数组中每次选择一个最小的插入到前面即可

冒泡排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n - i; j++) {
                if (nums[j] > nums[j + 1])
                    swap(nums[j], nums[j + 1]);
            }
        }
        return nums;
    }
};

通过不断的交换，每次把前面最大的元素起上去

插入排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        for (int i = 1; i < n; i++) {
            int temp = nums[i];
            int j = i - 1;
            while (j >= 0 && temp < nums[j]) {
                nums[j + 1] = nums[j];
                j--;
            }
            nums[j + 1] = temp;
        }
        return nums;
    }
};

对于每一个新的元素，将其插入到前面已经有序的数组中

这个写法是看起来复杂一点但是速度快一点的，之后可以在希尔排序看到另一种写法，区别只是在于插入有序数组的过程

快速排序

快速排序有很多写法

挖坑填数版本

class Solution {
public:
    void quick_sort(int l, int r, vector<int> &nums) {
        if (l >= r) return;
        int k = rand() % (r - l + 1) + l;
        int i = l, j = r;
        while (i < j) {
            while (i < j && nums[j] > nums[k]) j--;
            if (i < j) swap(nums[j], nums[k]), k = j;
            while (i < j && nums[i] <= nums[k]) i++;
            if (i < j) swap(nums[i], nums[k]), k = i;
        }
        while (i > l && nums[i] == nums[i - 1]) i--;
        while (j < r && nums[j] == nums[j + 1]) j++;
        quick_sort(l, i - 1, nums);
        quick_sort(j + 1, r, nums);
    }
    vector<int> sortArray(vector<int>& nums) {
        quick_sort(0, nums.size() - 1, nums);
        return nums;
    }
};

个人不太推荐这种写法，主要是要注意的细节太多了，一不小心写错了就没了

对于这种模板来说，需要判断的越少越好

class Solution {
public:
    void quick_sort(int l, int r, vector<int> &nums) {
        if (l >= r) return;
        int k = rand() % (r - l + 1) + l;
        swap(nums[k], nums[r]);
        int i = l - 1;
        for (int j = l; j < r; j++) {
            if (nums[j] <= nums[r]) {
                i++;
                swap(nums[i], nums[j]);
            }
        }
        swap(nums[i + 1], nums[r]);
        int ll = i + 1, rr = i + 1;
        while (ll > l && nums[ll] == nums[ll - 1]) ll--;
        while (rr < r && nums[rr] == nums[rr + 1]) rr++;
        quick_sort(l, ll - 1, nums);
        quick_sort(rr + 1, r, nums);
    }
    vector<int> sortArray(vector<int>& nums) {
        quick_sort(0, nums.size() - 1, nums);
        return nums;
    }
};

这个版本的虽然看起来臃肿了一些，但是思路清晰，如果不了解具体过程可以看一下leetcode的官方题解，里面有演示动画，一看就懂

两种写法个人都加了重复元素的判断，防止算法在含有较多重复元素的时候退化，主要是为了过洛谷的数据

归并排序

归并排序的思路简单，而且是稳定复杂度不会退化的，还可以用来排序链表，推荐

class Solution {
public:
    vector<int> tmp;
    void merge_sort(vector<int> &nums, int l, int r) {
        if (l >= r) return;
        int mid = (l + r) / 2;
        merge_sort(nums, l, mid);
        merge_sort(nums, mid + 1, r);
        int i = l, j = mid + 1, cnt = 0;
        while (i <= mid && j <= r) {
            if (nums[i] < nums[j]) tmp[cnt++] = nums[i++];
            else tmp[cnt++] = nums[j++];
        }
        while (i <= mid) tmp[cnt++] = nums[i++];
        while (j <= r) tmp[cnt++] = nums[j++];
        for (int i = 0; i < cnt; i++) {
            nums[l + i] = tmp[i];
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        tmp.resize(nums.size());
        merge_sort(nums, 0, nums.size() - 1);
        return nums;
    }
};

堆排序

堆排序唯一要说的就是注意初始化时候的顺序，题解里的堆排序写的有点长，不方便当做模板记忆，所以我就改造了一下

class Solution {
public:
    void adjust(vector<int> &nums, int i, int len) {
        while (i * 2 + 1 <= len) {
            int nxt = i * 2 + 1;
            if (nxt + 1 <= len && nums[nxt] < nums[nxt + 1]) nxt++;
            if (nums[nxt] < nums[i]) return;
            swap(nums[i], nums[nxt]);
            i = nxt;
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        for (int i = n / 2; i >= 0; i--) adjust(nums, i, n - 1);
        for (int i = n - 1; i >= 1; i--) {
            swap(nums[i], nums[0]);
            adjust(nums, 0, i - 1);
        }
        return nums;
    }
};

为什么在初始化的时候要逆序，因为在调整上层节点的时候需要保证下面的节点已经满足了堆的性质，否则你在交换的时候交换的就不一定是最大值，所以自底向上

希尔排序

建议gap就是每次除2

这个写法就是和上面的插入排序相对应的写法，减少了swap的次数，可以提高效率

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        int gap = n / 2;
        while (gap > 0) {
            for (int i = 0; i < gap; i++) {
                for (int j = i + gap; j < n; j += gap) {
                    int k = j - gap, temp = nums[j];
                    while (k >= i && nums[k] > temp) {
                        nums[k + gap] = nums[k];
                        k -= gap;
                    }
                    nums[k + gap] = temp;
                }
            }
            gap /= 2;
        }
        return nums;
    }
};

这个就是比较简单的基于swap的写法，主要小心数组越界，其实效率差不了多少，这个也比较好写

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        int gap = n / 2;
        while (gap > 0) {
            for (int i = 0; i < gap; i++) {
                for (int j = i + gap; j < n; j += gap) {
                    int temp = j;
                    while (temp > i && nums[temp] < nums[temp - gap]) {
                        swap(nums[temp], nums[temp - gap]);
                        temp -= gap;
                    }
                }
            }
            gap /= 2;
        }
        return nums;
    }
};

基数排序

这个实现比较巧妙，建议多看一下理解

cnt开到19是因为有负数，即[-9, 9]

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int maxx = 0, exp = 1, n = nums.size();
        for (const auto &x : nums) maxx = max(maxx, abs(x));
        vector<int> buffer(n);
        while (exp <= maxx) {
            vector<int> cnt(19, 0);
            for (const auto &x : nums) {
                cnt[(x / exp) % 10 + 9]++;
            }
            for (int i = 1; i < 19; i++) {
                cnt[i] += cnt[i - 1];   //通过这里计算前缀和
            }
            for (int i = n - 1; i >= 0; i--) {
                int digit = (nums[i] / exp) % 10 + 9;
                buffer[cnt[digit] - 1] = nums[i];//-1是因为下标从0开始
                cnt[digit]--;
            }
            copy(buffer.begin(), buffer.end(), nums.begin());
            exp *= 10;
        }
        return nums;
    }
};