Daily C/C++ 接雨水
leetcode的题,这道题算是十分经典的一道题了,有很多种解法
对于单调栈的做法来说,我们维护的是每个元素两边比他大的第一个元素的值以及位置,然后用值乘上这两个比他大的元素划分出来的范围,就是结果
这种做法更像是把答案用高度来进行横向的切割
而更加简单的思路是维护每个元素的两边的最大值,然后每个元素的贡献就是两个最大值之间较小的那一个减去当前元素的高度
这种做法是把答案纵向切割,单独考虑每个位置,长度永远就都是1
这里想说的是维护最大值的算法的一个优化版,就是利用双指针维护最大值
那为什么这道题可以用双指针来做呢?首先我们要明白,双指针是在帮助我们快速计算当前元素左右两边的最大值中的较小的那一个是谁
可以知道,左最大leftmax,也就是当前元素到左边第一个元素中的最大值是一个随着下标增加而递增的函数,因为我们是不断在找下一个更大的元素
同理,右最大则是随着下标递减而递增的函数
画出这个图来看一下
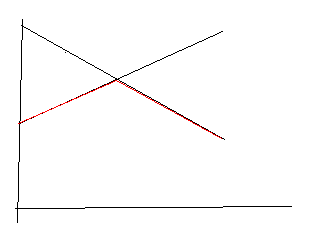
他们是有一个交点的,同时,我们每次需要的两个元素的较小值,也就是红色部分
假设我们当前在左边这半块,那么我们实际上就只需要左最大来更新答案,也就是对于每个元素的贡献就是 leftmax - a[i]
所以问题看似转化为了我们要怎么找到这个交点,然后交点的左边,我们用左最大更新,交点的右边用右最大更新
但是这个交点是比较难找的
我们要做的就是利用双指针找到这个点
我们同时维护左指针的左最大和右指针的右最大,那么当左最大比较大的时候,我们移动右边的指针,并期望右指针可以找到一个更大的右最大。
更具体的来说
对于当前的两个指针lptr和rptr,lptr就是左最大的位置,同时我们有a[lptr] > a[rptr], 对于这种情况,我们可以放心的用右最大值来更新右指针上元素的贡献
可以这样去想,两个指针开始都在端点处,然后左指针找到了左最大,并且左最大大于右最大的情况下,右指针开始向左移动,并在路径上更新元素的贡献,直到找到一个值大于左最大,这时右指针更新右最大,并且定在这里开始等待左指针。这时候右最大是大于左最大的,我们开始移动左指针,直到他又找到了一个新的元素大于当前右指针的元素,也就是大于右最大
可以发现,算法的过程实际上就是两个指针在两端出发,随着红色线的轨迹一点一点向上移动,两个指针会等待对方,所以我们就可以逐步逼近最终的交点
所以我们就可以放心的在路径上进行更新。
关键点在于理解,两个指针的移动实际上是以双方最大值的更新来交替进行的。
文章评论