现代计算机图形学 作业7 解析(3)
这次终于到了微表面模型,在成功实现了这个模型后,我们就可以将渲染的质量再提高一个档次
在开始之前,如果感兴趣的同学可以先看一下这两篇文章 链接 链接 主要实现的原理就是基于这两篇文章。我这里只是给做一个总结,所以还是推荐综合起来一起看。
这里因为是总结性的文章,所以我这里也就不再多给大家贴公式或者讲原理什么的了
之前我们说过,当成功的把path tracing的代码写完以后,基本上就不需要再去调整什么了,因为微表面模型相关的优化都是在材质上实现的
同样的,能够影响我们的就是之前主要提过的三个函数,即sample,pdf和eval。
这里首先我们要实现的就是eval,因为eval就是我们渲染方程的BRDF。我们可以这样想,目前的eval是返回一个基于材质的常数,所以无论在那个方向,返回的都是固定的,所以体现的就是漫反射的性质。而对于sample和pdf来说,无论你怎么改变他,其实是与我们后面的计算有关的,即蒙特卡洛积分等,并不能直接的体现出光线在这个材质上反射的性质。所以在成功修正了eval以后,我们就可以看到初步的结果。
这里贴出BRDF
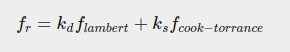
那么对于微表面模型,首先要处理三个量,即半程向量的分布,几何遮盖,以及菲涅尔项。
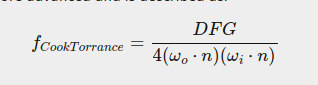
其中对于菲涅尔项,体现的是光反射的系数,所以也就会被认定为是我们渲染方程中的ks
然后对于半程向量的分布,是基于我们的法线以及表面的粗糙程度的,这里贴出代码
inline double distributionGGX(const Vector3f &normal, const Vector3f &h, double rough_ness) {
double a2 = rough_ness * rough_ness;
double nDotH = std::max(dotProduct(normal, h), 0.0f);
double nDotH2 = nDotH * nDotH;
double denom = nDotH2 * (a2 - 1.0f) + 1.0f;
denom = M_PI * denom * denom;
return a2 / denom;
}
比如表面越粗糙,那么分布的半程向量肯定就越分散,这样就可以体现出漫反射的性质。而如果表面光滑,那么半程向量肯定就会集中于法向量的方向,让我们的表面呈现镜面反射的性质。因为记住,我们是有了出射方向和入射方向,才得到的半程向量。半程向量体现的就是表面中有多少微表面可以让我们进行反射。
然后就是几何遮挡,就是说微表面中互相遮挡的现象,其实就是基于粗糙程度的一个函数,上面的文章中有实现,就不再贴代码。
然后就是菲涅尔项,体现的是不同视角对于反射光线的影响。这里注意就是每个材质有一个基础反射率,然后在不同的视角下,菲涅尔项可以给我们一个基于基础反射率的反射系数。
其中有一个细节就是对于金属材质的基础反射率的计算,我们要进行一个插值,因为金属性越强反射的也就越强,这里大家还是看一下原文的细节。
我这里贴出代码
double cos1 = std::max(dotProduct(N, wo), 0.0f);
double cos2 = std::max(dotProduct(N, wi), 0.0f);
if (cos1 > 0.0f && cos2 > 0.0f) {
Vector3f h = (wi + wo).normalized();
double k = pow((roughness + 1.0f), 2) / 8.0f;
double distribute = distributionGGX(N, h, roughness);
double geometry = geometrySmith(N, wo, wi, k);
Vector3f fresnel = fresnelSchlick(cos1, F0);
Vector3f Ks = fresnel;
Vector3f Kd = (Vector3f(1.0f) - Ks) * (1.0f - metallic);
return Kd * albedo / M_PI + Ks * distribute * geometry / std::max((double)0.0001f, (4.0f * cos1 * cos2));
}
通过代码可以看到,我们的ks就是菲涅尔项,决定了反射的系数,我们还需要遵守能量守恒,即反射项加上吸收项不能大于1,这里kd就表示吸收的光,也就是漫反射系数。这里的代码增强了金属反射的影响,即认定金属基本不会进行漫反射,会把所有的光都反射出去,所以kd也与金属性有关
然后实现完成后大家的图应该是类似这个样子

有很多的噪点,如果大家尝试添加几个材质,然后用金属性比较强的材质的话,就会发现反射并没有发生
就是类似这个样子

这个原因在上面的文章中也提过了,就是因为在我们的积分收敛速度太慢了。固然我们的实现是正确的,但是由于收敛速度过慢导致了我们在低spp的情况下不能得到正确的结果
那么这里就要涉及到重要性采样了。可以这样理解,我们在采样的时候,如果随机变量和我们原本要积分的点越相近,得到的结果的估计误差就越小。所以我们需要一种新的采样方法来帮我们有更好的收敛速度
那么对于数学推导这方面,我也看不太懂,所以就是搬过来公式直接翻译成代码。
如果大家想直觉性的理解的话,就是对于粗糙程度低的表面,采样就更多的去采样镜面反射的光线。这样就可以契合我们的BRDF。
而对于采样的概率,也就是pdf的话,其实也可以想到就是和半程向量的概率有关,因为求的是采样到该出射光线的概率。然后有一个点就是这里

我们的BRDF里是求的半程向量的概率,但是他不等于反射光线的概率,因为相同的半程向量对应的出射入射的光线可能不同,所以我们要求采样的光线的概率,也就有了这个变化。
然后大家实现了以后,可能会发现一个问题,图片里面有大量的白点。这个我猜测可能是因为某些地方的浮点数导致的。考虑光线的合理性,对于一个光线来说,他最大得到的值就是0到1,比如我们其中有一束光线得到了一个很大的值,他就会影响到这个像素的最终结果。所以我们每次将光线clamp在0到1之间,这样可以解决光线过亮的问题
那么最后,就可以得到我们的结果

文章评论